Question

12．已知：二次函数y=x²-2x-3．
（1）运用对称性，画出这个二次函数图象；
（2）当x满足条件x＜-1或x＞2条件时，y≥0，不等式-x²+2x+3＞0的解集为-1＜x＜3；
（3）当-1＜x＜4时，求y的取值范围是-4≤y＜5．

Answer 1

分析 （1）首先求得函数顶点坐标和对称轴，以及函数与x轴的交点坐标，据此即可作出函数图象；
（2）根据函数图象即可直接写出x的范围；
（3）对称轴在-1和4之间，然后确定-1和4哪个离对称轴较远，里用图象确定y的范围．

解答 解：（1）函数的对称轴是x=1，
当x=1时，y=1-2-3=-4，则顶点坐标是（1，-4）．
令y=0，则x²-2x-3=0，解得x₁=3，x₂=-1．
则函数与x轴的交点坐标是（3，0）和（-1，0）．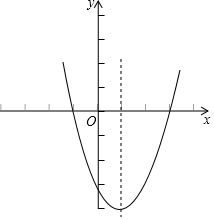
；
（2）当x＜-1或x＞2时，y≥0；
不等式-x²+2x+3＞0，即x²-2x+3＜0的解集为：-1＜x＜3．
故答案是：x＜-1或x＞2，-1＜x＜3；
（3）当x=4时，y=16-8-3=5，则y的取值范围是：-4≤y＜5．
故答案是：-4≤y＜5．

点评 本题考查了二次函数的对称性，以及利用函数图象解决实际问题，考查了数形结合思想的实际应用．