题目内容
 两条直线与两坐标轴的交点如图所示,则图中阴影图形的面积为
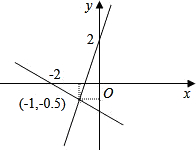
两条直线与两坐标轴的交点如图所示,则图中阴影图形的面积为
- A.4
- B.2
- C.1
- D.以上都不对
B
分析:根据直角坐标系中各点的坐标可得到阴影图形的底边为2,高为2,然后根据三角形面积公式计算.
解答:图中阴影图形的面积= ×2×2=2.
×2×2=2.
故选B.
点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.
分析:根据直角坐标系中各点的坐标可得到阴影图形的底边为2,高为2,然后根据三角形面积公式计算.
解答:图中阴影图形的面积=
 ×2×2=2.
×2×2=2.故选B.
点评:本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 写出如图所示的直线解析式
写出如图所示的直线解析式 两条直线与两坐标轴的交点如图所示,则图中阴影图形的面积为( )
两条直线与两坐标轴的交点如图所示,则图中阴影图形的面积为( ) 写出如图所示的直线解析式________,图中两条直线与两坐标轴所围成的面积是________.
写出如图所示的直线解析式________,图中两条直线与两坐标轴所围成的面积是________.