题目内容
⊙O的半径为2,△ABC是⊙O的内接三角形,弧AB所对的圆周角为45°,圆心O到BC的距离为1,则AC的长为________.
 +
+
分析:先过点O作OE⊥AC,OF⊥BC,过点B作BD⊥AC,求出∠AOB=90°,∠CBD=45°,得出AB=2
 ,∠OBA=45°,再求出BF=
,∠OBA=45°,再求出BF= ,∠OBF=30°,BC=2
,∠OBF=30°,BC=2 ,∠OBD=45°-30°=15°,最后根据∠ABD=30°,得出AD=
,∠OBD=45°-30°=15°,最后根据∠ABD=30°,得出AD= ,BD=
,BD= ,即可求出AC.
,即可求出AC.解答:过点O作OE⊥AC,OF⊥BC,过点B作BD⊥AC,

∵弧AB所对的圆周角为45°,
∴∠AOB=90°,∠CBD=45°
∴AB=
 =2
=2 ,∠OBA=45°,
,∠OBA=45°,∵OF=1,
∴BF=
 =
= ,∠OBF=30°,
,∠OBF=30°,∴BC=2
 ,∠OBD=45°-30°=15°,
,∠OBD=45°-30°=15°,∴∠ABD=30°,
∴AD=
 ×2
×2 =
= ,
,BD=
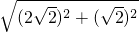 =
= ,
,∴CD=
 ,
,∴AC=
 +
+ .
.故答案为:
 +
+ .
.点评:此题考查了垂经定理和圆周角定理,解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离.
如图,⊙O的半径为13cm,弦AB∥CD,两弦位于圆心O的两侧,AB=24cm,CD=10cm,求AB和CD的距离. 如图,⊙P内含于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP.若⊙O的半径为3,⊙P的半径为1,则弦AB的长为
如图,⊙P内含于⊙O,⊙O的弦AB与⊙P相切,且AB∥OP.若⊙O的半径为3,⊙P的半径为1,则弦AB的长为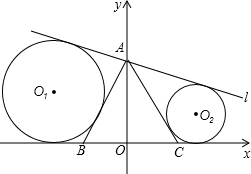
 如图,已知四边形ABCD外接⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,求△ABD的面积.
如图,已知四边形ABCD外接⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE•AC,BD=8,求△ABD的面积.