Question

【题目】△ABC中，∠ACB=90°，CB=6,AC=8,点D是AC上的一点，点E是BD上一点.

（1）如图（1），若点D在AB的垂直平分线上，求CD的长.

（2）如图（2），连接AE，若AE平分∠BAC，BE平分∠ABC，求点E到AC的距离.

（3）若点E到三角形两边的距离为1.5，求CD的长.（直接写出答案）

Answer 1

【答案】（1）（2）2（3）3或2或

【解析】

(1)由垂直平分线的性质可得BD=AD,AE=BE=5,设CD长为x，在中，由勾股定理列出方程即可解出CD的长；

(2)过点E作EF⊥AC于点F，EM⊥AB于点M，EN⊥BC于点N，由角平分线的性质可得EF=EM=EN,AE、BE、CE将分割成三个三角形，利用面积关系= 可求出EF的长即为所求；

(3)根据题意可分三种情况讨论：①当点E到AB和BC的距离为1.5时，过点D作DF⊥AB于点F，设CD为x,在中利用勾股定理可列出方程，求出x；②当点E到CB和CA的距离为1.5时，过点E作EM⊥AC于点M，EN⊥BC于点N，易知四边形CMEN为正方形，可得CM=1.5，由EM∥BC,可得，进而得到,代入数据即可求出CD；③当点E到AB和AC的距离为1.5时，过点E作EM⊥AB于点M，EN⊥AC于点N，EF⊥BC于点F，易知四边形CNEF为矩形，根据面积关系= 可求EF的长度即为CN的长度，由EN∥BC,可得进而可得,代入数据即可求出CD的长度.

(1)如图所示，设AB的垂直平分线为DE，垂足为E，

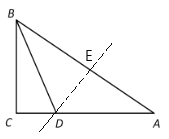
∵∠ACB=90°，CB=6,AC=8,

∴AB==10，

∵DE垂直平分AB，

∴BD=AD,AE=BE=AB=5,

设CD=x，则AD=BD=8-x，在中，由勾股定理可得：

，

解得：，

∴点D在AB的垂直平分线上时，CD= ；

(2)如图所示，过点E作EF⊥AC于点F，EM⊥AB于点M，EN⊥BC于点N，连接CE，

∵AE平分∠BAC,EF⊥AC,EM⊥AB,

∴EF=EM,

∵BE平分∠ABC,EM⊥AB,EN⊥BC,

∴EM=EN,

∴EF=EM=EN,

设EF=EM=EN=x，则：

=

即：×AC×BC= ×AC×EF+ ×AB×EM+ ×BC×EN,

6×8=8x+10x+6x，

解得：x=2，

∴点E到AC的距离为2；

(3)根据题意可分三种情况：

①如图所示，当点E到AB和BC的距离为1.5时，此时点E在∠CBA的角平分线上，即BD平分∠CBA，过点D作DF⊥AB于点F，

∵BD平分∠CBA，DF⊥AB,DC⊥BC,

∴CD=DF,

又∵∠C=∠DFB=90°,BD=BD,

∴(HL),

∴BF=BC=6,

∴AF=4,

设CD=x,则DF=x,AD=8-x,在中，由勾股定理可得：

，

解得:x=3,

∴当点E到AB和BC的距离为1.5时，CD=3;

②如图所示，当点E到CB和CA的距离为1.5时，此时点E在∠BCA的角平分线上，即CE平分∠BCA，过点E作EM⊥AC于点M，EN⊥BC于点N，此时EM=EN=1.5,EM∥BC,

∵∠NCM=90°, EM⊥AC，EN⊥BC，

∴四边形CMEN为矩形，

∵EM=EN

∴矩形CMEN为正方形，

∴CM=1.5，

设CD=x,则DM=x-1.5，

∵EM∥BC,

∴

∴,

即: ，

解得：x=2，

∴当点E到CB和CA的距离为1.5时，CD=2;

③如图所示，当点E到AB和AC的距离为1.5时，此时点E在∠BAC的角平分线上，即AE平分∠BAC，过点E作EM⊥AB于点M，EN⊥AC于点N，EF⊥BC于点F，此时EM=EN=1.5,四边形CNEF为矩形，

∵= ，

∴×AC×BC= ×AC×EN+ ×AB×EM+ ×BC×EF,

即6×8=8×1.5+10×1.5+6×EF,

解得：EF=,

∵四边形CNEF为矩形，

∴CN= EF=,

设CD=x,则DN=x-，

∵EN∥BC,

∴

∴,

即: ，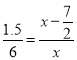

解得：x=，

∴当点E到AB和AC的距离为1.5时，CD= .

综上所述，若点E到三角形两边的距离为1.5，CD的长为3或2或.