Question

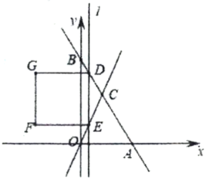
【题目】如图，直线分别与轴、轴交于、两点，与直线交于点，平行于轴的直线从原点出发，以每秒1个单位长度的速度沿轴向右平移，直线分别交直线、直线于点、，以为边向左侧作正方形，当直线经过点时停止运动，设直线的运动时间为（秒）．

（1）________，________；

（2）设线段的长度为（）；求与之间的函数关系式；

（3）当正方形的边落在轴上时，求出的值．

Answer 1

【答案】（1）8，2；（2）与之间的函数关系式为：；（3）或．

【解析】

（1）将点C分别代入两个函数，可求得b、k的值；

（2）存在两种情况，直线在点C的左侧和直线在点C的右侧，分别用t表示出D、E的坐标，可得出DE的长度；

（3）GF在y轴上，意味着点F在y轴上，则EF=t，然后根据EF=d得出t的值．

（1）∵直线分别与轴、轴交于、两点，与直线交于点

∴4=2k，4=－2×2+b

解得：，．

（2）∵直线的解析式为，直线的解析式为

在中，令，得，

∴，

令，得，解得，

∴，

∵，，

∴当时，

当时，

综上所述，与之间的函数关系式为：；

（3）∵四边形是正方形

∴

当时，，解得，

当时，，解得；

综上所述，当正方形的边落在轴上时，或；