题目内容
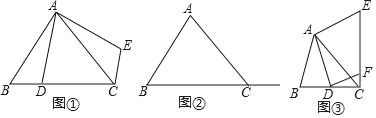
【题目】如图,将一张直角三角形纸片![]() 沿斜边
沿斜边![]() 上的中线
上的中线![]() 剪开,得到
剪开,得到![]() ,再将
,再将![]() 沿
沿![]() 方向平移到
方向平移到![]() 的位置,若从平移开始到点
的位置,若从平移开始到点![]() 未到达点
未到达点![]() 时,
时,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
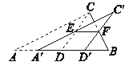
(1)试探究![]() 的形状,请说明理由;
的形状,请说明理由;
(2)当四边形![]() 为菱形时,判断
为菱形时,判断![]() 与
与![]() 是否全等,请说明理由.
是否全等,请说明理由.
【答案】(1)![]() 是等腰三角形,见解析;(2)全等,见解析.
是等腰三角形,见解析;(2)全等,见解析.
【解析】
(1)先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.
(2)根据四边形EDD′F为菱形得到EF=DE=DA′,EF∥DD′,即可推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.
(1) ![]() 是等腰三角形.
是等腰三角形.
理由:∵![]() 是直角三角形,
是直角三角形,![]() ,
,![]() 是中线,
是中线,
∴![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰三角形.
是等腰三角形.
(2)全等.理由如下:
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
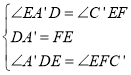
∴![]() ≌
≌![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目