题目内容
9. 如图,已知∠CBD=∠ACB,要说明△ABC≌△DCB,
如图,已知∠CBD=∠ACB,要说明△ABC≌△DCB,(1)若以“SAS”为依据,则需添加一个条件是BD=AC;
(2)若以“AAS”为依据,则需添加一个条件是∠BAC=∠CDB;
(3)若以“ASA”为依据,则需添加一个条件是∠BCD=∠CBD;
请选择一种方法进行证明.
分析 (1)已有条件∠CBD=∠ACB和公共边BC=BC,以“SAS”为依据,则需添加一个条件BD=AC;
(2)已有条件∠CBD=∠ACB和公共边BC=BC,以“AAS”为依据,则需添加一个条件∠BAC=∠CDB;
(3)已有条件∠CBD=∠ACB和公共边BC=BC,以“ASA”为依据,则需添加一个条件∠BCD=∠CBD.
解答 解:(1)添加条件BD=AC,
∵在△ABC和△DCB中$\left\{\begin{array}{l}{BC=BC}\\{∠CBD=∠ACB}\\{BD=AC}\end{array}\right.$,
∴△ABC≌△DCB(SAS),
故答案为:BD=AC;
(2)添加条件∠BAC=∠CDB,
∵在△ABC和△DCB中$\left\{\begin{array}{l}{∠CBD=∠ACB}\\{∠BAC=∠CDB}\\{BC=BC}\end{array}\right.$,
∴△ABC≌△DCB(AAS),
故答案为:∠BAC=∠CDB;
(3)添加∠BCD=∠CBD,
∵在△ABC和△DCB中$\left\{\begin{array}{l}{∠CBD=∠ACB}\\{BC=BC}\\{∠BCD=∠CBD}\end{array}\right.$
∴△ABC≌△DCB(ASA),
故答案为:∠BCD=∠CBD.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
相关题目
19. 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆,如图线段AB的最小覆盖圆就是以线段AB为直径的圆,△ABC的最小覆盖圆是其外接圆,那么长为8cm、宽为6cm的矩形的最小覆盖圆半径是( )
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆,如图线段AB的最小覆盖圆就是以线段AB为直径的圆,△ABC的最小覆盖圆是其外接圆,那么长为8cm、宽为6cm的矩形的最小覆盖圆半径是( )
 我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆,如图线段AB的最小覆盖圆就是以线段AB为直径的圆,△ABC的最小覆盖圆是其外接圆,那么长为8cm、宽为6cm的矩形的最小覆盖圆半径是( )
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆,如图线段AB的最小覆盖圆就是以线段AB为直径的圆,△ABC的最小覆盖圆是其外接圆,那么长为8cm、宽为6cm的矩形的最小覆盖圆半径是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 5cm |
20.在$\frac{22}{7}$,$\sqrt{8}$,-3.1416,π,$\sqrt{25}$,0.161161116…,$\root{3}{9}$中无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
1.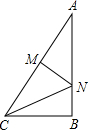 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
 如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )
如图,在Rt△ABC中,∠B=90°,AC=10,BC=6,线段AC的垂直平分线MN分别交AC、AB于M、N两点,则CN的长为( )| A. | $\frac{35}{8}$ | B. | $\frac{25}{4}$ | C. | $\frac{25}{2}$ | D. | 7 |
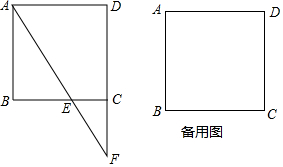 已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.
已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连结AE交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B1处.