题目内容
已知反比例函数y=
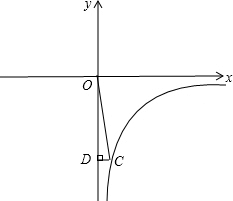
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3,若直线y=ax+b经过点A,并且经过反比例函数y=
的图象上另一点C(n,-
),
(1)求反比例函数的解析式和直线y=ax+b解析式;
﹙2﹚求△AOC的面积;
(3)在坐标轴上是否存在一点P,使△PAO为等腰三角形?若存在,请直接写出P点坐标;若不存在,说明理由.

| k |
| x |
| k |
| x |
| 3 |
| 2 |
(1)求反比例函数的解析式和直线y=ax+b解析式;
﹙2﹚求△AOC的面积;
(3)在坐标轴上是否存在一点P,使△PAO为等腰三角形?若存在,请直接写出P点坐标;若不存在,说明理由.

(1)在Rt△OAB中,OB=2,S△OAB=3,
∴AB=3,
即A(-2,3),
∴反比例函数的解析式为y=-
| 6 |
| x |
∴C(4,-
| 3 |
| 2 |
设直线AC的解析式为y=kx+b,则有:
|

解得:
|
∴y=-
| 3 |
| 4 |
| 3 |
| 2 |
(2)根据(1)y=-
| 3 |
| 4 |
| 3 |
| 2 |
得M(2,0),
∴OM=2,
∴S△AOC=S△AOM+S△OCM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)存在.
∵A(-2,3),
∴OA=
| 13 |
当OA=OP时,P1(0,
| 13 |
| 13 |
| 13 |
| 13 |
当OA=AP时,P5(0,6)、P6(-4,0);
当AP=OP时,P7(0,
| 13 |
| 6 |
| 13 |
| 4 |

练习册系列答案
相关题目







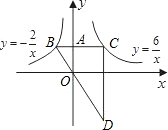 <0)的图象于B,交函数y=
<0)的图象于B,交函数y=