题目内容
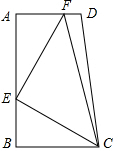 (2013•海珠区一模)如图,在直角梯形ABCD中,∠A=∠B=90°,AD=5,AB=10,BC=6,点E是线段AB上的动点,连结CE,EF⊥CE交AD于F,连结CF,设BE=x.
(2013•海珠区一模)如图,在直角梯形ABCD中,∠A=∠B=90°,AD=5,AB=10,BC=6,点E是线段AB上的动点,连结CE,EF⊥CE交AD于F,连结CF,设BE=x.(1)当∠BCE=30°时,求△BCE的周长;
(2)当x=5时,求证:CF=AF+BC;
(3)是否存在x,使得CF=
| 2 |
分析:(1)在直角△BCE中利用三角函数即可求得BE,EC的长度,则三角形的周长即可求得;
(2)取FC的中点P,连接E、P,易证EP是直角梯形ABCF的中位线,以及直角三角形的性质,以及梯形的中位线定理即可证得;
(3)取AB的中点Q,连接Q、P,则QP是直角梯形ABCF的中位线,QP=
,EP是Rt△EFC斜边上的中线,EP=
,要使得CF=
(AF+BC),只需EP=
QP,即Rt△PQE是等腰直角三角形,即可表示出FA、AE的长度,然后根据Rt△EBC∽Rt△FAE,相似三角形的对应边的比相等可以得到关于x的方程,从而求解.
(2)取FC的中点P,连接E、P,易证EP是直角梯形ABCF的中位线,以及直角三角形的性质,以及梯形的中位线定理即可证得;
(3)取AB的中点Q,连接Q、P,则QP是直角梯形ABCF的中位线,QP=
| AF+BC |
| 2 |
| CF |
| 2 |
| 2 |
| 2 |
解答:解:(1)如图:∵∠A=∠B=90°,BC=6,BE=x,∠BCE=30°
∴Rt△EBC中,BE=BCtan30°=2
,EC=
=4
∴△BCE的周长=BC+EB+EC=6+6
(2)如图:取FC的中点P,连接EP,
∵∠A=∠B=90°,AD=5,AB=10,BC=6,BE=x=5,EF⊥CE,
∴EP是直角梯形ABCF的中位线,EP=
EP也是Rt△EFC斜边上的中线,EP=
∴EP=
=
,即CF=AF+BC
(3)如图:取AB的中点Q,连接QP,
∵∠A=∠B=90°,AD=5,AB=10,BC=6,BE=x,EF⊥CE,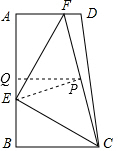
∴AE=10-x,QE=|5-x|,∠AFE+∠AEF=90°,∠BEC+∠AEF=90°
QP是直角梯形ABCF的中位线,QP=
,∠PQE=90°
EP是Rt△EFC斜边上的中线,EP=
要使得CF=
(AF+BC),只需EP=
QP,即Rt△PQE是等腰直角三角形,QP=QE=|5-x|
∴AF=2QP-BC=2|5-x|-6
∵∠A=∠B=90°,EF⊥CE,
∴∠AFE+∠AEF=90°,∠BEC+∠AEF=90°
∴∠AFE=∠BEC
∴Rt△EBC∽Rt△FAE
∴
=
,即
=
当0≤x≤5时,|5-x|=5-x,2|5-x|-6=4-2x
=
,x1=11+
(舍),x2=11-
当5<x≤10时,|5-x|=x-5,2|5-x|-6=2x-16
=
,x1=-1+
,x2=-1-
(舍)
综上所述:x=11-
或-1+
时,CF=
(AF+BC)
∴Rt△EBC中,BE=BCtan30°=2
| 3 |
| BC |
| cos300 |
| 3 |
∴△BCE的周长=BC+EB+EC=6+6
| 3 |
(2)如图:取FC的中点P,连接EP,
∵∠A=∠B=90°,AD=5,AB=10,BC=6,BE=x=5,EF⊥CE,
∴EP是直角梯形ABCF的中位线,EP=
| AF+BC |
| 2 |
EP也是Rt△EFC斜边上的中线,EP=
| CF |
| 2 |
∴EP=
| AF+BC |
| 2 |
| CF |
| 2 |
(3)如图:取AB的中点Q,连接QP,
∵∠A=∠B=90°,AD=5,AB=10,BC=6,BE=x,EF⊥CE,

∴AE=10-x,QE=|5-x|,∠AFE+∠AEF=90°,∠BEC+∠AEF=90°
QP是直角梯形ABCF的中位线,QP=
| AF+BC |
| 2 |
EP是Rt△EFC斜边上的中线,EP=
| CF |
| 2 |
要使得CF=
| 2 |
| 2 |
∴AF=2QP-BC=2|5-x|-6
∵∠A=∠B=90°,EF⊥CE,
∴∠AFE+∠AEF=90°,∠BEC+∠AEF=90°
∴∠AFE=∠BEC
∴Rt△EBC∽Rt△FAE
∴
| EB |
| FA |
| BC |
| AE |
| x |
| 2|5-x|-6 |
| 6 |
| 10-x |
当0≤x≤5时,|5-x|=5-x,2|5-x|-6=4-2x
| x |
| 4-2x |
| 6 |
| 10-x |
| 97 |
| 97 |
当5<x≤10时,|5-x|=x-5,2|5-x|-6=2x-16
| x |
| 2x-16 |
| 6 |
| 10-x |
| 97 |
| 97 |
综上所述:x=11-
| 97 |
| 97 |
| 2 |
点评:本题是相似三角形的判定与性质,以及直角三角形的性质,梯形的中位线定理的综合应用,正确作出辅助线是关键.

练习册系列答案
相关题目
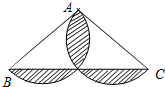 (2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
(2013•海珠区一模)如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )