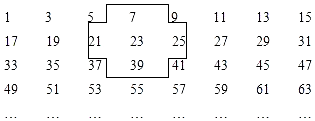
题目内容
11.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为an,计算a1+a2,a2+a3,a3+a4,…由此推算a19+a20=400.分析 首先计算a1+a2,a2+a3,a3+a4的值,然后总结规律,根据规律可以得出结论.
解答 解:∵a1+a2=4,
a2+a3=9,
a3+a4=16,
…
∴an+an+1=(n+1)2=n2+2n+1,
∴当n=19时,a19+a20=202=400.
故答案为:400.
点评 此题考查数字的变化规律,由特殊计算a1+a2,a2+a3,a3+a4的值可以发现规律:an+an+1=(n+1)2,发现规律是解决本题的关键.

练习册系列答案
相关题目
1.用一个平面去截一个几何体,截面形状为三角形,则这个几何体不可能为( )
| A. | 立方体 | B. | 圆柱 | C. | 圆锥 | D. | 正三棱柱 |
19.下列图案中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列函数是二次函数的是( )
| A. | y=2x+2 | B. | y=-2x | C. | y=x2+2 | D. | y=x-2 |
3.下列图形中,不是轴对称图形的是( )
| A. | 线段 | B. | 角 | ||
| C. | 等腰三角形 | D. | 有30°角的直角三角形 |