Question

【题目】如图，在中，点，分别是，的中点，连接，，，且，过点作交的延长线于点.

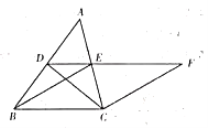
（1）求证：四边形是菱形；

（2）在不添加任何辅助线和字母的情况下，请直接写出图中与面积相等的所有三角形（不包括）.

Answer 1

【答案】（1）证明见解析；（2）、、、.

【解析】

（1）由题意易得，EF与BC平行，结合，可得四边形BCFE是平行四边形，然后求出邻边，则四边形BCFE是菱形；

（2）根据等底等高的两个三角形面积相等以及三角形的中线将三角形分成面积相等的两部分进行求解即可．

（1）证明：∵、分别是、的中点，

∴，，

∵，

∴四边形是平行四边形，

∵，，

∴，

∴平行四边形是菱形；

（2）解：①∵由（1）知，四边形BCFE是菱形，

∴BC＝FE，BC∥EF，

∴△FEC与△BEC是等底等高的两个三角形，

∴S△FEC＝S△BEC；

②△AEB与△BEC是等底同高的两个三角形，则S△AEB＝S△BEC；

③S△ADC＝S△ABC，S△BEC＝S△ABC，则S△ADC＝S△BEC；

④S△BDC＝S△ABC，S△BEC＝S△ABC，则S△BDC＝S△BEC．

综上所述，与△BEC面积相等的三角形有：△FEC、△AEB、△ADC、△BDC．