题目内容
一次函数y=ax+b的图象过点P(1,2),且与x轴交于点A,与y轴交于点B,若tan∠PAO= ,则点B的坐标是________.
,则点B的坐标是________.
(0, ),(0,
),(0, )
)
分析:设A点坐标为(x,0),过点P作PD⊥x轴于点D,则AD=|x-1|,PD=2,根据tan∠PAO= 即可求出x的值,进而得出一次函数y=ax+b的解析式,求出此函数与y轴的交点坐标即可.
即可求出x的值,进而得出一次函数y=ax+b的解析式,求出此函数与y轴的交点坐标即可.
解答: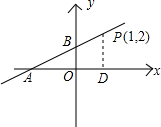 解:如图所示:设A点坐标为(x,0),过点P作PD⊥x轴于点D,
解:如图所示:设A点坐标为(x,0),过点P作PD⊥x轴于点D,
∵P(1,2),
∴PD=2,
∵tan∠PAO= ,
,
∴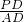 =
= ,即
,即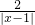 =
= ,
,
解得x=5或x=-3,
当x=5时,A(5,0),
∵一次函数y=ax+b的图象过A(5,0)、P(1,2)两点,
∴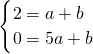 ,
,
解得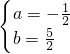 ,
,
∴此一次函数的解析式为:y=- x+
x+ ,
,
当x=-3时,
一次函数y=ax+b的图象过A(-3,0)、P(1,2)两点,
∴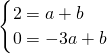 ,
,
解得 ,
,
∴B的坐标是(0, )(0,
)(0, ),
),
故答案为(0, ),(0,
),(0, ).
).
点评:本题考查了待定系数法求一次函数解析式及解直角三角形的相关知识,综合性较强,要注意进行分类讨论.
 ),(0,
),(0, )
)分析:设A点坐标为(x,0),过点P作PD⊥x轴于点D,则AD=|x-1|,PD=2,根据tan∠PAO=
 即可求出x的值,进而得出一次函数y=ax+b的解析式,求出此函数与y轴的交点坐标即可.
即可求出x的值,进而得出一次函数y=ax+b的解析式,求出此函数与y轴的交点坐标即可.解答:
 解:如图所示:设A点坐标为(x,0),过点P作PD⊥x轴于点D,
解:如图所示:设A点坐标为(x,0),过点P作PD⊥x轴于点D,∵P(1,2),
∴PD=2,
∵tan∠PAO=
 ,
,∴
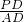 =
= ,即
,即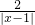 =
= ,
,解得x=5或x=-3,
当x=5时,A(5,0),
∵一次函数y=ax+b的图象过A(5,0)、P(1,2)两点,
∴
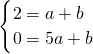 ,
,解得
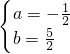 ,
,∴此一次函数的解析式为:y=-
 x+
x+ ,
,当x=-3时,
一次函数y=ax+b的图象过A(-3,0)、P(1,2)两点,
∴
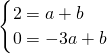 ,
,解得
 ,
,∴B的坐标是(0,
 )(0,
)(0, ),
),故答案为(0,
 ),(0,
),(0, ).
).点评:本题考查了待定系数法求一次函数解析式及解直角三角形的相关知识,综合性较强,要注意进行分类讨论.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
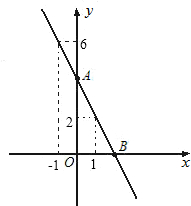 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: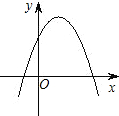 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=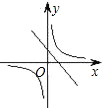
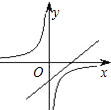
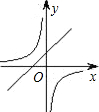
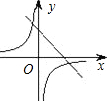
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=