题目内容
16. 如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD,则四边形AOCD的面积是( )
如图,以平行四边形ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AD,则四边形AOCD的面积是( )| A. | 6 | B. | 7 | C. | 9 | D. | 10 |
分析 先求出反比例函数和直线BC的解析式,再求出由两个解析式组成方程组的解,得出点D的坐标,得出D为BC的中点,△ABD的面积=$\frac{1}{4}$平行四边形ABCD的面积,即可求出四边形AOCD的面积.
解答 解:∵四边形ABCD是平行四边形,A、C的坐标分别是(2,4)、(3,0),
∴点B的坐标为:(5,4),
把点A(2,4)代入反比例函数y=$\frac{k}{x}$得:k=8,
∴反比例函数的解析式为:y=$\frac{8}{x}$;
设直线BC的解析式为:y=kx+b,
把点B(5,4),C(3,0)代入得:$\left\{\begin{array}{l}{5k+b=4}\\{3k+b=0}\end{array}\right.$,
解得:k=2,b=-6,
∴直线BC的解析式为:y=2x-6,
解方程组$\left\{\begin{array}{l}{y=2x-6}\\{y=\frac{8}{x}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,或 $\left\{\begin{array}{l}{x=-1}\\{y=-8}\end{array}\right.$(不合题意,舍去),
∴点D的坐标为:(4,2),
即D为BC的中点,
∴△ABD的面积=$\frac{1}{4}$平行四边形ABCD的面积,
∴四边形AOCD的面积=平行四边形ABCO的面积-△ABD的面积=3×4-$\frac{1}{4}$×3×4=9.
故选C.
点评 本题考查了平行四边形的性质、用待定系数法求一次函数的解析式、平行四边形和三角形面积的计算;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
| A. | x2+5x-1=x(x+5)-1 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | x2-x+$\frac{1}{4}$=(x-$\frac{1}{2}$)2 | D. | 4x2-y2=(4x+y)(4x-y) |
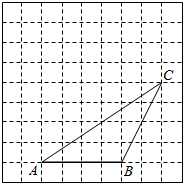 已知,如图,在正方形网格中,每个小正方形的边长均为1,将△ABC先向上平移3格,再向左平移2格.
已知,如图,在正方形网格中,每个小正方形的边长均为1,将△ABC先向上平移3格,再向左平移2格.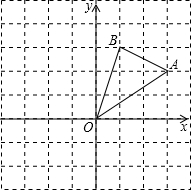 如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3). 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,交CD于E,已知∠1=40°,求∠2的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠AEF,交CD于E,已知∠1=40°,求∠2的度数.