Question

如图，在△ABC中，D、E分别是边AC、BC上的点，若△ADB≌△EDB≌△EDC，则∠C的度数为(     )

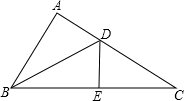
A．15°   B．20°    C．25°   D．30°

 

Answer 1

D【考点】全等三角形的性质．

【分析】根据全等三角形对应角相等，∠A=∠BED=∠CED，∠ABD=∠EBD=∠C，根据∠BED+∠CED=180°，可以得到∠A=∠BED=∠CED=90°，再利用三角形的内角和定理求解即可．

【解答】解：∵△ADB≌△EDB≌△EDC

∴∠A=∠BED=∠CED，∠ABD=∠EBD=∠C

∵∠BED+∠CED=180°

∴∠A=∠BED=∠CED=90°

在△ABC中，∠C+2∠C+90°=180°

∴∠C=30°

故选D．

【点评】本题主要考查全等三角形对应角相等的性质，做题时求出∠A=∠BED=∠CED=90°是正确解本题的突破口．