题目内容
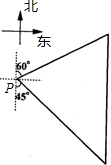 如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为________海里(结果保留根号).
如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为________海里(结果保留根号).
40
分析:过点P作PC⊥AB,垂足为C,根据题意可得∠APC=30°,∠BPC=45°,AP=80海里,然后在Rt△APC中可表示出PC,在Rt△PCB中可表示出PB,进而可得出答案.
解答: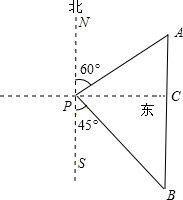 解:过点P作PC⊥AB,垂足为C,
解:过点P作PC⊥AB,垂足为C,
∵∠APN=60°,∠BPS=45°,
∴∠APC=30°,∠BPC=45°,
∵AP=80海里,
在Rt△APC中,
∵cos∠APC= ,
,
∴PC=PA•cos∠APC=80× =40
=40 ,
,
在Rt△PCB中,cos∠BPC=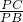 ,
,
PB= =
=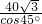 =40
=40 (海里)
(海里)
答:渔船所在的B处与海洋观测站P的距离为40 海里.
海里.
点评:本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

分析:过点P作PC⊥AB,垂足为C,根据题意可得∠APC=30°,∠BPC=45°,AP=80海里,然后在Rt△APC中可表示出PC,在Rt△PCB中可表示出PB,进而可得出答案.
解答:
 解:过点P作PC⊥AB,垂足为C,
解:过点P作PC⊥AB,垂足为C,∵∠APN=60°,∠BPS=45°,
∴∠APC=30°,∠BPC=45°,
∵AP=80海里,
在Rt△APC中,
∵cos∠APC=
 ,
,∴PC=PA•cos∠APC=80×
 =40
=40 ,
,在Rt△PCB中,cos∠BPC=
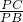 ,
,PB=
 =
=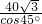 =40
=40 (海里)
(海里)答:渔船所在的B处与海洋观测站P的距离为40
 海里.
海里.点评:本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形,利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
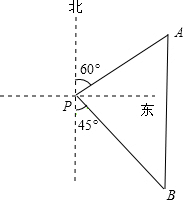 如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号). (2012•道里区一模)如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为
(2012•道里区一模)如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为

