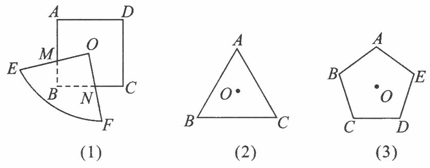
题目内容
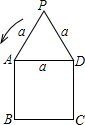 如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为
如图,等边三角形和正方形的边长都是a,在图形所在的平面内,将△PAD以点A为中心沿逆时针方向旋转,使AP与AB重合,如此继续分别以点B、C、D 为中心将三角形进行旋转,使点P回到原来位置为止,则点P从开始到结束所经过路径的长为
- A.
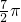 a
a - B.
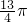 a
a - C.
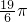 a
a - D.
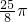 a
a
C
分析:首先作出图形,于是可得点P所经过的路径是半径为a、圆心角分别为210°和210°和150°的三段圆弧,根据弧长公式即可求出总长度.
解答: 解:作图如右:
解:作图如右:
点P所经过的路径是半径为a、圆心角分别为210°和210°和150°的三段圆弧,
故总长度为2πa( ×2+
×2+ )=
)=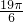 a.
a.
故选C.
点评:本题主要考查弧长的计算和等边三角形的性质,解答本题的关键是熟练掌握旋转的性质,此题难度不大.
分析:首先作出图形,于是可得点P所经过的路径是半径为a、圆心角分别为210°和210°和150°的三段圆弧,根据弧长公式即可求出总长度.
解答:
 解:作图如右:
解:作图如右:点P所经过的路径是半径为a、圆心角分别为210°和210°和150°的三段圆弧,
故总长度为2πa(
 ×2+
×2+ )=
)=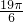 a.
a.故选C.
点评:本题主要考查弧长的计算和等边三角形的性质,解答本题的关键是熟练掌握旋转的性质,此题难度不大.

练习册系列答案
相关题目
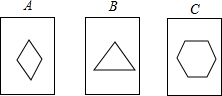 次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)
次抽到纸牌上的图形都为既是中心对称图形又是轴对称图形的概率(纸牌用A、B、C表示)