题目内容
| . |
| abc…xyz |
解；当y≤z时，|a-b|+|b-c|+…+|x-y|+|y-z|=z-a，当z=9，a=1 时取得最大值8．
当y＞z时，|a-b|+|b-c|+…+|x-y|+|y-z|=2y-a-z
当y=9，a=1，z=0 时取得最大值17．
所以|a-b|+|b-c|+…+|x-y|+|y-z|的最大值是17．
故答案为：17．
当y＞z时，|a-b|+|b-c|+…+|x-y|+|y-z|=2y-a-z
当y=9，a=1，z=0 时取得最大值17．
所以|a-b|+|b-c|+…+|x-y|+|y-z|的最大值是17．
故答案为：17．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
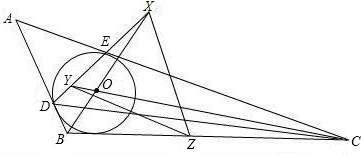O切于点E，BO与DE交于点X，CO与DE交于点Y，点Z是BC的中点．
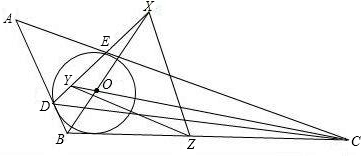O切于点E，BO与DE交于点X，CO与DE交于点Y，点Z是BC的中点．