题目内容
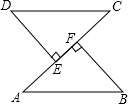 已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,AE=CF.
已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E、F,AE=CF.求证:
(1)DE=BF;
(2)AB∥CD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由AE=CF,利用等式的性质得到AF=CE,利用HL得到直角三角形CDE与直角三角形ABF全等,利用全等三角形的对应边相等即可得证;
(2)由全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
(2)由全等三角形的对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答:证明:(1)∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△CDE和Rt△ABF中,
,
∴Rt△CDE≌Rt△ABF(HL),
∴DE=BF;
(2)∵△CDE≌△ABF,
∴∠C=∠A,
∴DC∥AB.
∴AE+EF=CF+EF,即AF=CE,
在Rt△CDE和Rt△ABF中,
|
∴Rt△CDE≌Rt△ABF(HL),
∴DE=BF;
(2)∵△CDE≌△ABF,
∴∠C=∠A,
∴DC∥AB.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列各组数中互为相反数的是( )
A、-2与
| ||||
B、-2与
| ||||
C、2与(-
| ||||
D、|-
|
设a>0,b>0,则下列运算错误的是( )
A、
| ||||||||||
B、
| ||||||||||
C、(
| ||||||||||
D、
|
等腰三角形的两边长分别为5cm和10cm,则此三角形的周长是( )
| A、15cm |
| B、20cm |
| C、25cm |
| D、20cm或25cm |
 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题: