题目内容
矩形纸片ABCD中，AB=4，AD=8，将纸片沿EF折叠使点B与点D重合，折痕EF与BD相交于点O，则DF的长为
- A.3
- B.4
- C.5
- D.6
C
分析：设DF=x，则BF=x，CF=8-x，在RT△DFC中利用勾股定理可得出x的值，继而得出答案．
解答：设DF=x，则BF=x，CF=8-x，
在RT△DFC中，DF2=CF2+DC2，即x2=（8-x）2+42，
解得：x=5，即DF的长为5．
故选C．
点评：此题考查了翻折变换的知识，设出DF的长度，得出CF的长，然后在RT△DFC中利用勾股定理是解答本题的关键．
分析：设DF=x，则BF=x，CF=8-x，在RT△DFC中利用勾股定理可得出x的值，继而得出答案．
解答：设DF=x，则BF=x，CF=8-x，
在RT△DFC中，DF2=CF2+DC2，即x2=（8-x）2+42，
解得：x=5，即DF的长为5．
故选C．
点评：此题考查了翻折变换的知识，设出DF的长度，得出CF的长，然后在RT△DFC中利用勾股定理是解答本题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
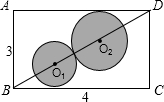如图，矩形纸片ABCD中，AB=3cm，BC=4cm，若要在该纸片中剪下两个外切的圆⊙O1和⊙O2，要求⊙O1和⊙O2的圆心均在对角线BD上，且⊙O1和⊙O2分别与BC、AD相切，则O1O2的长为（ ）
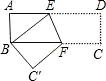如图，矩形纸片ABCD中，AD=9，AB=3，将其折叠，使点D与点B重合，折痕为EF，那么折痕EF的长为
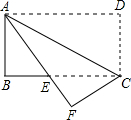如图，在矩形纸片ABCD中，将矩形纸片沿着对角线AC折叠，使点D落在点F处，设AF与BC相交于点E．
