题目内容
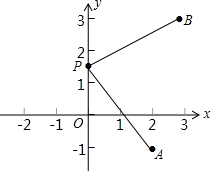 平面直角坐标系内有A(2,-1),B(3,3)两点,点P是y轴上一动点,求P到A、B距离之和最小时的坐标.
平面直角坐标系内有A(2,-1),B(3,3)两点,点P是y轴上一动点,求P到A、B距离之和最小时的坐标.
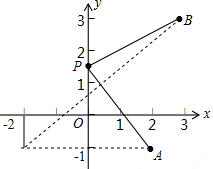 解:如图,作点A关于y轴的对称点C(-2,-1),连接CB,
解:如图,作点A关于y轴的对称点C(-2,-1),连接CB,设过C,B两点的直线函数关系式为y=kx+b,
∵C(-2,-1).B(3,3),
∴
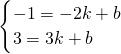 ,
,解得:
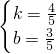 ,
,∴过C,B两点的直线函数关系式为y=
 x+
x+ ;
;当x=0时,y=
 ,
,即:直线CB与y轴交于点(0,
 ),
),∴P点坐标是(0,
 ).
).分析:首先作点A关于y轴的对称点C连接CB,CB与y轴交点即为P点,先求出过C,B两点的直线函数关系式,再求出直线与y轴交点坐标即可.
点评:此题主要考查了求一次函数关系式,以及轴对称求最短路线,关键是作出点A关于y轴的对称点C,求出过C,B两点的直线函数关系式.

练习册系列答案
相关题目
在平面直角坐标系内有线段AB、CD,其中A(3,1),B(4,3),C(6,2),D(8,6),若CD上有一点P的坐标为(a,b),则直线OP与AB的交点的坐标为
(
a,
b)
| 1 |
| 2 |
| 1 |
| 2 |
(
a,
b)
.| 1 |
| 2 |
| 1 |
| 2 |
 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围.