题目内容
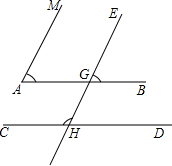
26、已知，如图∠BAM=75°，∠BGE=75°，∠CHG=105°，可得到AM∥EF，AB∥CE，试完成下列填空．解：∵∠BAM=75°，∠BGE=75°（
已知
）∴∠BAM=∠BGE（
等量代换
）∴
AM
∥EF
（同位角相等，两直线平行）又∵∠AGH=∠BGE（
对顶角相等
）∴∠AGH=75°（
等量代换
）∴∠AGH+∠CHG=75°+105°=180°（
等式性质
）∴
AB
∥CD
（同旁内角互补，两直线平行）分析：结合图形，根据同位角相等两直线平行可得AM∥EF，利用同旁内角互补两直线平行可证AB∥CD．
解答：解：∵∠BAM=75°，∠BGE=75°（已知），
∴∠BAM=∠BGE（等量代换），
∴AM∥EF（同位角相等，两直线平行）；
又∵∠AGH=∠BGE（对顶角相等），
∴∠AGH=75°（等量代换），
∴∠AGH+∠CHG=75°+105°=180°（等式性质），
∴AB∥CD（同旁内角互补，两直线平行）．
∴∠BAM=∠BGE（等量代换），
∴AM∥EF（同位角相等，两直线平行）；
又∵∠AGH=∠BGE（对顶角相等），
∴∠AGH=75°（等量代换），
∴∠AGH+∠CHG=75°+105°=180°（等式性质），
∴AB∥CD（同旁内角互补，两直线平行）．
点评：本题重点考查平行线的判定，要准确掌握平行线的判定定理．
练习册系列答案
相关题目
25、已知：如图，AM是△ABC的中线，∠DAM=∠BAM，CD∥AB．
