题目内容
1．
如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的动点，M为线段EF上一动点，则BM+DM最小值为6cm．
分析 连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．
解答 
解：连接AD，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×AD=12，解得AD=6cm，
∵EF是线段AB的垂直平分线，
∴点B关于直线EF的对称点为点A，
∴AD的长为BM+MD的最小值，
∴BM+DM最小值为6cm，
故答案为：6cm．
点评 本题考查的是轴对称-最短路线问题，熟知等腰三角形三线合一的性质是解答此题的关键．
练习册系列答案
相关题目
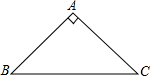如图，在△ABC中，AB=AC，∠BAC=90°，点D为射线CB上一点，连接AD，以AD为一边在AD右侧作正方形ADEF，直线EF与直线BC交于点M，若AB=2$\sqrt{2}$，BD=1，则CM的长为$\frac{1}{2}$或$\frac{3}{2}$．
如图所示，抛物线y=x2-4x+3与x轴分别交于A、B两点，交y轴于点C，
16．将抛物线y=-3x2+2向左平移1个单位，再向下平移3个单位后所得到的抛物线为（ ）
| A． | y=-3（x-1）2-3 | B． | y=-3（x-1）2-1 | C． | y=-3（x=1）2-3 | D． | y=-3（x+1）2-1 |