题目内容
19.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a,如:1☆3=1×32+2×1×3+1=16(1)求(-2)☆3的值;
(2)若($\frac{a+1}{2}$☆3)☆(-$\frac{1}{2}$)=8,求a的值;
(3)若2☆x=m,($\frac{1}{4}$x)☆3=n(其中x为有理数),试用x表示m-n.
分析 (1)原式利用已知的新定义计算即可得到结果;
(2)已知等式利用已知新定义化简求出a即可;
(3)已知等式利用已知新定义化简,表示出m-n即可.
解答 解:(1)根据题意得:原式=-18-12-2=-32;
(2)已知等式整理得:[$\frac{9}{2}$(a+1)+3(a+1)+$\frac{a+1}{2}$]×(-$\frac{1}{2}$)2-[$\frac{9}{2}$(a+1)+3(a+1)+$\frac{a+1}{2}$]+[$\frac{9}{2}$(a+1)+3(a+1)+$\frac{a+1}{2}$]=8,
即2(a+1)=8,
解得:a=3;
(3)已知等式整理得:2x2+4x+2=m,$\frac{9}{4}$x+$\frac{3}{2}$x+$\frac{1}{4}$x=n,即4x=n,
则m-n=2x2+2.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.若|a-$\frac{1}{2}$|+(2b+1)2=0,则a2+b2的值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.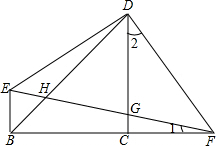 如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,
如图,等腰Rt△BCD中,∠BCD=90°,BC=CD,EB⊥BC,Rt△EDF中,∠EDF=90°,B、C、F在一条直线上,