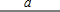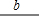题目内容
新定义：平行于三角形一边的直线被其他两边所截得的线段叫做“三角形的弦”，已知等边三角形的一条弦的长度为2cm，且这条弦将等边三角形分成面积相等的两个部分，那么这个等边三角形的边长为 cm．
考点：相似三角形的判定与性质,等边三角形的性质
专题：新定义
分析：首先根据题意画出图形，由DE∥BC，可得△ADE∽△ABC，然后由相似三角形面积比等于相似比的平方，求得答案．
解答：
解：如图，根据题意得：DE∥BC，且S△ADE=S四边形BCED，
∴△ADE∽△ABC，S△ADE：S△ABC=1：2，
∴DE：BC=1：
，
∵DE=2cm，
∴BC=2
cm，
即这个等边三角形的边长为：2
cm．
故答案为：2
．
解：如图，根据题意得：DE∥BC，且S△ADE=S四边形BCED，∴△ADE∽△ABC，S△ADE：S△ABC=1：2，
∴DE：BC=1：
| 2 |
∵DE=2cm，
∴BC=2
| 2 |
即这个等边三角形的边长为：2
| 2 |
故答案为：2
| 2 |
点评：此题考查了相似三角形的判定与性质．此题难度适中，属于新定义题，解题的关键是理解三角形的弦的定义．
练习册系列答案
相关题目
