题目内容
 △ABC中,∠ABC、∠ACB的平分线相交于点O;
△ABC中,∠ABC、∠ACB的平分线相交于点O;(1)若∠ABC=40°,∠ACB=50°,则∠BOC=
(2)若∠ABC+∠ACB=116°,则∠BOC=
(3)若∠A=76°,则∠BOC=
(4)若∠BOC=120°,则∠A=
(5)若∠A=x°,求∠BOC的度数(用x的代数式表示).
分析:(1)-(4)充分利用三角形的内角和定理和角平分线的定义进行求解;
(5)根据三角形的内角和定理以及角平分线的定义导出∠BOC=90°+0.5x.
(5)根据三角形的内角和定理以及角平分线的定义导出∠BOC=90°+0.5x.
解答:解:(1)∠BOC=180°-
(40°+50°)=135°;
(2)∠BOC=180°-
×116°=122°;
(3)∠BOC=180°-
×(180°-∠A)=128°;
(4)∵∠BOC=120°
∴∠OBC+∠OCB=60°
根据角平分线的定义得:∠ABC+∠ACB=2×60°=120°
∴∠A=60°;
(5)根据角平分线的定义得:∠OBC+∠OCB=
(∠ABC+∠ACB)
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
(∠ABC+∠ACB)=180°-
(180°-∠A)=90°+0.5x.
| 1 |
| 2 |
(2)∠BOC=180°-
| 1 |
| 2 |
(3)∠BOC=180°-
| 1 |
| 2 |
(4)∵∠BOC=120°
∴∠OBC+∠OCB=60°
根据角平分线的定义得:∠ABC+∠ACB=2×60°=120°
∴∠A=60°;
(5)根据角平分线的定义得:∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=180°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:通过做此题,主要是能够发现结论:△ABC中,∠ABC、∠ACB的平分线相交于点O,则∠BOC=90°+
∠A.
| 1 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
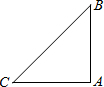 20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.
20、问题:已知△ABC中,∠BAC=2∠ACB,点D是△ABC内的一点,且AD=CD,BD=BA.探究∠DBC与∠ABC度数的比值.