题目内容
△ABC中,BC=10,AB= ,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为 .
,∠ABC=30°,点P在直线AC上,点P到直线AB的距离为1,则CP的长为 .
【答案】分析:过点C作CD⊥AB交BA的延长线于点D,根据∠ABC的正弦和余弦可以求出CD、BD的长度,从而可以求出AD的长度,然后利用勾股定理即可求出AC的长度,再利用相似三角形对应边成比例列式求出AP的长度,再分点P在线段AC上与点P在射线CA上两种情况讨论求解.
解答: 解:如图,过点C作CD⊥AB交BA的延长线于点D,
解:如图,过点C作CD⊥AB交BA的延长线于点D,
∵BC=10,∠ABC=30°,
∴CD=BCsin30°=5,
BD=BCcos30°=5 ,
,
∵AB= ,
,
∴AD=BD-AB=5 -4
-4 =
= ,
,
在Rt△ACD中,AC= =
= =2
=2 .
.
过P作PE⊥AB,与BA的延长线于点E,
∵点P在直线AC上,点P到直线AB的距离为1,
∴△APE∽△ACD,
∴ =
= ,
,
即 =
= ,
,
解得AP= ,
,
∴①点P在线段AC上时,CP=AC-AP=2 -
- =
= ,
,
②点P在射线CA上时,CP=AC+AP=2 +
+ =
= .
.
综上所述,CP的长为 或
或 .
.
故答案为: 或
或 .
.
点评:本题考查了解直角三角形,作出图形,利用好30°的角构造出直角三角形是解题的关键,要注意分情况讨论,避免漏解.
解答:
 解:如图,过点C作CD⊥AB交BA的延长线于点D,
解:如图,过点C作CD⊥AB交BA的延长线于点D,∵BC=10,∠ABC=30°,
∴CD=BCsin30°=5,
BD=BCcos30°=5
 ,
,∵AB=
 ,
,∴AD=BD-AB=5
 -4
-4 =
= ,
,在Rt△ACD中,AC=
 =
= =2
=2 .
.过P作PE⊥AB,与BA的延长线于点E,
∵点P在直线AC上,点P到直线AB的距离为1,
∴△APE∽△ACD,
∴
 =
= ,
,即
 =
= ,
,解得AP=
 ,
,∴①点P在线段AC上时,CP=AC-AP=2
 -
- =
= ,
,②点P在射线CA上时,CP=AC+AP=2
 +
+ =
= .
.综上所述,CP的长为
 或
或 .
.故答案为:
 或
或 .
.点评:本题考查了解直角三角形,作出图形,利用好30°的角构造出直角三角形是解题的关键,要注意分情况讨论,避免漏解.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
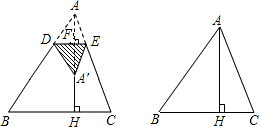 点A关于DE的对称点A′落在AH所在的直线上).
点A关于DE的对称点A′落在AH所在的直线上). 1、已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于
1、已知如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于 如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是
如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于E,交AC于F,点P是⊙A上的一点,且∠EPF=40°,则图中阴影部分的面积是 (2012•鄂州)在锐角三角形ABC中,BC=
(2012•鄂州)在锐角三角形ABC中,BC=