题目内容
【题目】已知![]() 的半径为
的半径为![]() ,弦
,弦![]() ,
,![]() ,
,![]() ,则
,则![]() 和
和![]() 的距离为________.
的距离为________.
【答案】14或2
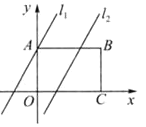
【解析】分两种情况:①当AB、CD在圆心O的两侧时,如图1,作辅助线,构建两个直角三角形,先由垂径定理得出BF和ED的长,再利用勾股定理计算出OE和OF的长,相加即可求出距离EF的长;
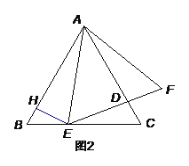
②当AB、CD在圆心O的同侧时,如图2,同理求得距离EF的长.
分两种情况:
①当AB、CD在圆心O的两侧时,如图1,过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
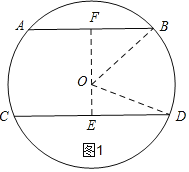
∵AB∥CD,
∴EF⊥AB,
∴ED=![]() CD,BF=
CD,BF=![]() AB,
AB,
∵AB=12,CD=16,
∴ED=![]() ×16=8,BF=
×16=8,BF=![]() ×12=6,
×12=6,
由勾股定理得:OE=![]() ,
,
OF=![]() ,
,
∴EF=OE+OF=6+8=14;
②当AB、CD在圆心O的同侧时,如图2,
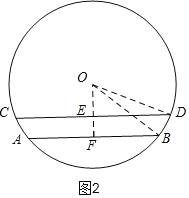
同理得:EF=OF-OE=8-6=2,
综上所述,AB和CD的距离为14或2.

练习册系列答案
相关题目
【题目】将长为![]() ,宽为
,宽为![]() 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为![]() .
.
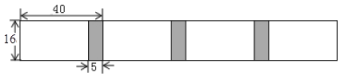
(1)根据图示,将下表补充完整;
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
(2)设![]() 张白纸粘合后的总长度为
张白纸粘合后的总长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为![]() 吗?为什么?
吗?为什么?