Question

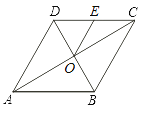
【题目】如图1，点E是等边△ABC的边BC上一点，以AE为边作等边△AEF，EF交AC于D.

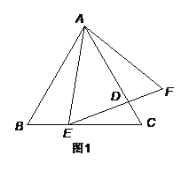
（1）连接CF，求证：

（2）如图2，作EH AF交AB于点H.

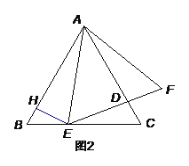
①求证：；

②若EH=2，ED=4，直接写出BE的长为 _________.

Answer 1

【答案】（1）证明见解析（2）见解析（3）

【解析】（1）由等边三角形的性质，根据两角对应相等的两三角形相似，再根据相似三角形的对应边成比例；

（2）①根据相似三角形的对应边成比例证明即可；

②可证EA=EH+ED=6, 作AM⊥BC于M，然后根据勾股定理求解.

（1）∵△ABC,△AEF都是等边三角形，∴AB=AC，∠AEF=∠C=600，

又∵∠EAD=∠CAE，,∴∽ , ∴

∵AB=AC ∴

（2）①∵EH∥AF , ∴∠AEH=∠EAF=60°=∠B

方法1：∵∽ ∴

又∽ , ∴

∴，即

②可证EA=EH+ED=6, 作AM⊥BC于M，可设BE=2x,EC=4x,则EM=x, ,

由勾股定理得,.