题目内容
【题目】如图,四条直线l1:y1= ![]() x,l2:y2=
x,l2:y2= ![]() x,l3:y3=﹣
x,l3:y3=﹣ ![]() x,l4:y4=﹣
x,l4:y4=﹣ ![]() x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 .
x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2 , 再过点A2作A2A3⊥l1交l2于点A3 , 再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为 . 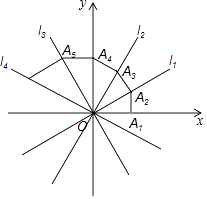
【答案】(( ![]() )2016,0)
)2016,0)
【解析】解:∵y1= ![]() x,l2:y2=
x,l2:y2= ![]() x,l3:y3=﹣
x,l3:y3=﹣ ![]() x,l4:y4=﹣
x,l4:y4=﹣ ![]() x,
x,
∴x轴、l1、l2、y轴、l3、l4依次相交为30的角,
∵2017=168×12+1,
∴点A2016在x轴的正半轴上,
∵OA2= ![]() =
= ![]() ,
,
OA3=( ![]() )2,
)2,
OA4=( ![]() )3,
)3,
…
OA2016=( ![]() )2015,
)2015,
∴点A2017坐标为(( ![]() )2016,0).
)2016,0).
所以答案是(( ![]() )2016,0).
)2016,0).
【考点精析】利用锐角三角函数的定义对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

练习册系列答案
相关题目