Question

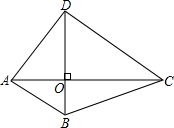如图；AC，BD是四边形ABCD的对角线，AC⊥BD于点O；
（1）求证：S_{四边形ABCD}=

1

2

AC•BD；
（2）若AC+BD=10，当AC，BD的长是多少时，四边形ABCD的面积最大？

Answer 1

分析：（1）把四边形ABCD分成△ABC和△ACD两部分，利用三角形的面积公式列式整理即可得证；
（2）设AC=x，表示出BD，再根据（1）的结论整理，然后利用二次函数的最值问题解答．

解答：（1）证明：∵AC⊥BD，
∴S_{四边形ABCD}=S_△ABC+S_△ACD，
=

1

2

AC•OB+

1

2

AC•OD，
=

1

2

AC（OB+OD）
=

1

2

AC•BD；

（2）解：设AC=x，∵AC+BD=10，
∴BD=10-x，
∴四边形ABCD的面积=

1

2

x（10-x）=-

1

2

（x²-10x）=-

1

2

（x-5）²+

25

2

，
∵-

1

2

＜0，
∴当x=5时，四边形ABCD的面积有最大值

25

2

，
此时AC=5，BD=5．

点评：本题考查了二次函数的最值问题，三角形的面积，把四边形的面积分成两个三角形的面积进行求解是解题的关键，也是此类题目常用的方法之一．