题目内容
如图,AD为等边△ABC底边上的中线,DM⊥AC,垂足为M,延长AC到E。使CE=CD,试问:点M是AE的中点吗?为什么?
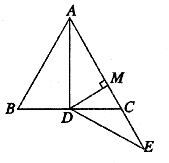
解:点M是AE的中点
∵△ABC是等边三角形
∴∠BAC=∠ACB=60º
∵AD为等边△ABC底边上的中线
∴∠DAC![]() (等腰三角形三线合一)
(等腰三角形三线合一)
∴CE=CD
∴∠CDE=∠E(等边对等角)
又∵∠CDE+∠E=∠ACB=60º
∴![]()
∴![]()
∴AD=DE(等角对等边)
又∵DM⊥AC
∴DM为等腰△ADE的中线(等腰三角形三线合一)
即点M是A层的中点

练习册系列答案
相关题目
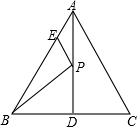 如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )
如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
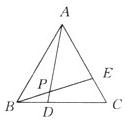 22、如图,△ABC为等边三角形,D、E分别是BC、AC上的一点,且BD=CE,AD和BE交于点P,求∠APE的度数.
22、如图,△ABC为等边三角形,D、E分别是BC、AC上的一点,且BD=CE,AD和BE交于点P,求∠APE的度数.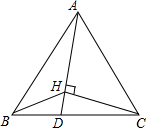 如图,D为等边△ABC的BC边上一点,已知BD=1,CD=2,CH⊥AD于点H,连接BH.试证:∠BHD=60°.
如图,D为等边△ABC的BC边上一点,已知BD=1,CD=2,CH⊥AD于点H,连接BH.试证:∠BHD=60°. 已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.
已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P.