题目内容
 如图,在一个正方形的四个顶点处,按逆时针方向各写了一个数:2,0,0,1.然后取各边中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两端点处的两个数的平均值.连续这样做到的10个正方形,则图上写出的所有数的和是( )
如图,在一个正方形的四个顶点处,按逆时针方向各写了一个数:2,0,0,1.然后取各边中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两端点处的两个数的平均值.连续这样做到的10个正方形,则图上写出的所有数的和是( )| A、30 | B、27 | C、20 | D、10 |
分析:根据已知可分别求得第一,二个正方形四个顶点的数的和,从而不难发现规律,根据规律解题即可.
解答:解:∵一个正方形的四个顶点处,按逆时针方向各写了一个数:2,0,0,1,
∴第一个正方形的四个顶点的和=2+0+0+1=3,
∵第二个正方形的四个顶点处的数分别是:1,0,
,
,
∴第二个正方形的四个顶点之和=1+0+
+
=3,
同理:第三个正方形的四个顶点之和=
+
+
+1=3,
∴可发现每个正方形的四个顶点之和均为3,
∵连续做到10个这样的正方形,
∴写出的所有数的和=10×3=30.
故选A.
∴第一个正方形的四个顶点的和=2+0+0+1=3,
∵第二个正方形的四个顶点处的数分别是:1,0,
| 1 |
| 2 |
| 3 |
| 2 |
∴第二个正方形的四个顶点之和=1+0+
| 1 |
| 2 |
| 3 |
| 2 |
同理:第三个正方形的四个顶点之和=
| 1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
∴可发现每个正方形的四个顶点之和均为3,
∵连续做到10个这样的正方形,
∴写出的所有数的和=10×3=30.
故选A.
点评:此题主要考查三角形中位线定理,关键是根据题意发现存在的规律.

练习册系列答案
相关题目
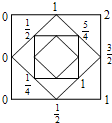 如图,在一个正方形的四个顶点处,按逆时针方向各写一个数:2,0,0,1,然后取各边的中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两个端点处的两个数的平均值.连续这样做到第十个正方形,则图上写出的所有数的和
如图,在一个正方形的四个顶点处,按逆时针方向各写一个数:2,0,0,1,然后取各边的中点,并在各中点处写上其所在边两端点处的两个数的平均值.这四个中点构成一个新的正方形,又在这个新的正方形四边中点处写上其所在边两个端点处的两个数的平均值.连续这样做到第十个正方形,则图上写出的所有数的和 (2009•河西区一模)如图,在一个正方形的工件中心挖去一个小正方形(小正方形的四边与大正方形的四边分别平方),留下一个“方环”,现在要想求这个方环的面积,但只准测量一次(即只准测一条线段的长),你能办到吗?请叙述你的方法:
(2009•河西区一模)如图,在一个正方形的工件中心挖去一个小正方形(小正方形的四边与大正方形的四边分别平方),留下一个“方环”,现在要想求这个方环的面积,但只准测量一次(即只准测一条线段的长),你能办到吗?请叙述你的方法:
