题目内容
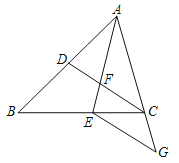
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,则
,则![]() 的内切圆
的内切圆![]() 与外接圆
与外接圆![]() 的周长之比为______.
的周长之比为______.
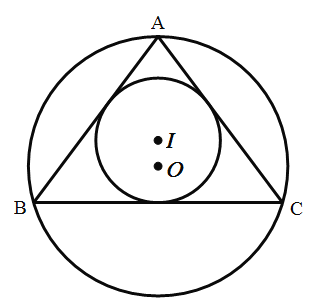
【答案】![]()
【解析】
过点A作AD⊥BC,过点E作EI⊥AB交AD于点I,过点F作AB的垂直平分线交AD于点O,再分别证△AEI∽△ADB和△AFO∽△ADB相似,求出EI和AO的长,再用圆的周长公式计算即可.
解:如图所示,
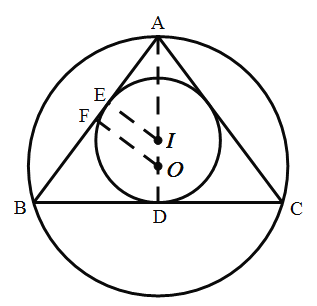
过点A作AD⊥BC,过点E作EI⊥AB交AD于点I,过点F作AB的垂直平分线交AD于点O,
∵![]() ,
,
∴EI,AO分别为内切圆![]() 与外接圆
与外接圆![]() 的半径,
的半径,
∵![]() ,
,
∴BD=3
∴AD=![]() ,
,
∵∠AEI=∠ADB,∠EAI=∠DAB,
∴△AEI∽△ADB,
∴![]() ,
,
∴EI=![]() ,
,
∵∠AFO=∠ADB,∠FAO=∠DAB,
∴△AFO∽△ADB,
∴![]()
∴AO=![]()
∴![]() 的内切圆
的内切圆![]() 与外接圆
与外接圆![]() 的周长之比为=(2π×
的周长之比为=(2π×![]() )∶(2π×
)∶(2π×![]() )=
)=![]() ,
,
故答案为![]() .
.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目