题目内容
把4a2-2a+1加上一个单项式 ，使其成为一个完全平方式（写出一个即可）．
考点：完全平方式
专题：开放型
分析：根据完全平方公式的公式结构分情况讨论求解即可．
解答：解：4a2-2a+1-3a2=a2-2a+1=（a-1）2，
4a2-2a+1-2a=4a2-4a+1=（2a-1）2，
4a2-2a+1+6a=4a2+4a+1=（2a+1）2，
4a2-2a+1-
=4a2-2a+
=（2a-
）2，
所以，加上的单项式为-3a2或-2a或6a或-
．
故答案为：-3a2或-2a或6a或-
．
4a2-2a+1-2a=4a2-4a+1=（2a-1）2，
4a2-2a+1+6a=4a2+4a+1=（2a+1）2，
4a2-2a+1-
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
所以，加上的单项式为-3a2或-2a或6a或-
| 3 |
| 4 |
故答案为：-3a2或-2a或6a或-
| 3 |
| 4 |
点评：本题考查了完全平方式，熟练掌握完全平方公式的公式结构是解题的关键，难点在于分情况讨论．
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
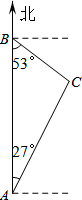如图，禁渔期间，我渔政船在A处发现正北方向B处有一艘可疑船只，测得A、B两处距离为99海里，可疑船只正沿南偏东53°方向航行．我渔政船迅速沿北偏东27°方向前去拦截，2小时后刚好在C处将可疑船只拦截．求该可疑船只航行的速度．
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米．某天该深潜器在海面下1800米的A点处作业（如图），测得正前方海底沉船C的俯角为45°，该深潜器在同一深度向正前方直线航行2000米到B点，此时测得海底沉船C的俯角为60°．
如图，⊙O与正方形ABCD的各边分别相切于点E、F、G、H，点P是
”的字样，则它T恤上的数字实际是
如图，过反比例函数y=在下列各数中是无理数的有（ ）
-0.333…，
，
，-π，
，3.1415，2.010101．
-0.333…，
| 2 |
| 4 |
| 22 |
| 7 |
| A、2个 | B、4个 | C、5个 | D、6个 |