题目内容
 已知如图所示,E、F是四边形ABCD对角线AC上的两点,AF=CE,DF=BE,DF∥BE.
已知如图所示,E、F是四边形ABCD对角线AC上的两点,AF=CE,DF=BE,DF∥BE.(1)求证:△AFD≌△CEB;
(2)四边形ABCD是平行四边形吗?请说明理由.
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)首先根据平行线的性质可得∠DFA=∠BEC,再加上AF=CE,DF=BE可利用SAS定理证明△AFD≌△CEB;
(2)首先根据△AFD≌△CEB可得AD=BC,∠DAC=∠ECB,然后证明AD∥CB,根据一组对边平行且相等的四边形是平行四边形可得结论.
(2)首先根据△AFD≌△CEB可得AD=BC,∠DAC=∠ECB,然后证明AD∥CB,根据一组对边平行且相等的四边形是平行四边形可得结论.
解答:(1)证明:∵DF∥BE,
∴∠DFA=∠BEC,
在△ADF和△CBE中,
,
∴△AFD≌△CEB(SAS);
(2)四边形ABCD是平行四边形,
∵△AFD≌△CEB,
∴AD=BC,∠DAC=∠ECB,
∴AD∥BC,
∴四边形ABCD是平行四边形.
∴∠DFA=∠BEC,
在△ADF和△CBE中,
|
∴△AFD≌△CEB(SAS);
(2)四边形ABCD是平行四边形,
∵△AFD≌△CEB,
∴AD=BC,∠DAC=∠ECB,
∴AD∥BC,
∴四边形ABCD是平行四边形.
点评:本题主要考查平行四边形的判定,全等三角形的判定与性质,关键是掌握一组对边平行且相等的四边形是平行四边形.

练习册系列答案
相关题目
圆柱的三视图是( )
| A、两个圆、一个长方形 |
| B、一个圆、两个长方形 |
| C、两个圆、一个三角形 |
| D、一个圆、两个三角形 |
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A、函数有最小值 | ||
| B、当-1<x<2时,y>0 | ||
C、当x<
| ||
D、对称轴是直线x=
|
下列说法正确的是( )
| A、无限小数都是无理数 |
| B、无理数都是无限小数 |
| C、有理数只是有限小数 |
| D、实数可以分为正实数和负实数 |
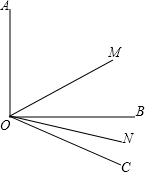 已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°
已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°
 如图所示,已知直线AB,CD相交于点O,OF平分∠BOC,∠DOE=90°,∠AOE=44°18°,求∠BOF和∠BOE的大小.
如图所示,已知直线AB,CD相交于点O,OF平分∠BOC,∠DOE=90°,∠AOE=44°18°,求∠BOF和∠BOE的大小. 如图,在⊙O中,
如图,在⊙O中,