题目内容
已知如图，直线y=﹣
x+4
与x轴相交于点A，与直线y=
x相交于点P．
（1）求点P的坐标；
（2）求S△OPA的值；
（3）动点E从原点O出发，沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，F的坐标为（a，0），矩形EBOF与△OPA重叠部分的面积为S．求：S与a之间的函数关系式．
x+4与x轴相交于点A，与直线y=x相交于点P．（1）求点P的坐标；
（2）求S△OPA的值；
（3）动点E从原点O出发，沿着O→P→A的路线向点A匀速运动（E不与点O、A重合），过点E分别作EF⊥x轴于F，EB⊥y轴于B．设运动t秒时，F的坐标为（a，0），矩形EBOF与△OPA重叠部分的面积为S．求：S与a之间的函数关系式．
解：（1）﹣
x+4
=
x
x=3，
y=
．
所以P（3，
）．
（2）0=﹣
x+4
．
x=4．
4×
×
=2
．
故面积为2
．
（3）当E点在OP上运动时，
∵F点的横坐标为a，所以纵坐标为
a，
∴S=
a*a﹣
×
a*a=
a2．
当点E在PA上运动时，
∵F点的横坐标为a，所以纵坐标为﹣
a+4
．
∴S=（﹣
a+4
）a﹣
（﹣
a+4
）a=﹣
a2+2
a．
x+4=xx=3，
y=
．所以P（3，
）．（2）0=﹣
x+4．x=4．
4×
×=2．故面积为2
．（3）当E点在OP上运动时，
∵F点的横坐标为a，所以纵坐标为
a，∴S=
a*a﹣×a*a=a2．当点E在PA上运动时，
∵F点的横坐标为a，所以纵坐标为﹣
a+4．∴S=（﹣
a+4）a﹣（﹣a+4）a=﹣a2+2a．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
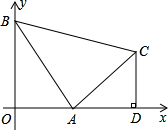腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
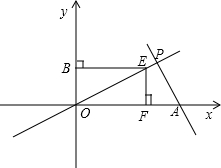已知如图，直线y=-
已知如图，直线l1∥l2∥l3∥l4，相邻两条平行线间的距离都等于h，若正方形ABCD的四个顶点分别在四条直线上，求它的面积．
已知如图：直线AB、CD被l所截，AB∥CD，EF平分∠CEG，GH平分∠BGE．求证：EF∥GH．
已知如图，直线AB、CD相交于O，∠AOC=50°，OE平分∠DOB，求∠COE的度数．