Question

如图，已知线段 AB 和 CD 的公共部分为 BD，且 BD=AB= CD，线段 AB、CD 的中点 E、F

之间距离是 20，求 AB、CD 的长．

Answer 1

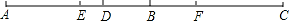
【考点】两点间的距离．

【分析】根据线段中点的性质，可得 AE=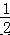AB，CF= CD，根据线段的和差，可得 AC 的长、EF 的 长，根据解方程，可得 x 的值．

【解答】解：设 BD=x，则 AB=3x，CD=4x．

^∵点 E、点 F 分别为 AB、CD 的中点，

^∴AE= 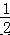AB=1.5x，CF= 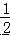CD=2x，

AC=AB+CD﹣BD=3x+4x﹣x=6x．

^∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5x．

^∵EF=20，

^∴2.5x=20， 解得：x=8．

^∴AB=3x=24，CD=4x=32．

【点评】本题考查了两点间的距离，利用 BD=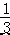AB= 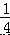CD 得出 BD=x，则 AB=3x，CD=4x，AC=6x

是解题关键．