题目内容
4.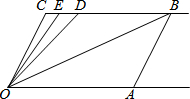 如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.
如图,射线OA∥射线CB,∠C=∠OAB=100°.点D、E在线段CB上,且∠DOB=∠BOA,OE平分∠DOC.(1)试说明AB∥OC的理由;
(2)试求∠BOE的度数;
(3)平移线段AB;
①试问∠OBC:∠ODC的值是否会发生变化?若不会,请求出这个比值;若会,请找出相应变化规律.
②若在平移过程中存在某种情况使得∠OEC=∠OBA,试求此时∠OEC的度数.
分析 (1)根据OA∥CB,得到∠OAB+∠ABC=180°,根据已知证明∠C+∠ABC=180°,证明结论;
(2)根据两直线平行,同旁内角互补求出∠AOC,然后求出∠EOB=$\frac{1}{2}$∠AOC,计算即可得解;
(3)根据两直线平行,内错角相等可得∠AOB=∠OBC,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ODC=2∠OBC,从而得解;根据三角形的内角和定理求出∠COE=∠AOB,从而得到OB、OE、OD是∠AOC的四等分线,再利用三角形的内角和定理列式计算即可得解.
解答 解:(1)∵OA∥CB,
∴∠OAB+∠ABC=180°,
∵∠C=∠OAB=100°,
∴∠C+∠ABC=180°,
∴AB∥OC
(2)∵CB∥OA,
∴∠AOC=180°-∠C=180°-100°=80°,
∵OE平分∠COD,
∴∠COE=∠EOD,
∵∠DOB=∠AOB,
∴∠EOB=∠EOD+∠DOB=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×80°=40°;
(3)①∵CB∥OA,
∴∠AOB=∠OBC,
∵∠DOB=∠AOB,
∴∠DOB=∠OBC,
∴∠ODC=∠DOB+∠OBC=2∠OBC,
∴∠OBC:∠ODC=1:2,是定值;
②在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=$\frac{1}{4}$∠AOC=$\frac{1}{4}$×80°=20°,
∴∠OEC=180°-∠C-∠COE=180°-100°-20°=60°,
∴∠OEC=∠OBA,此时∠OEC=∠OBA=60°
点评 本题考查了平行线的性质和判定的应用,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,此题是一道中档题目,难度适中.

| A. | $\left\{\begin{array}{l}{6y=6x+6}\\{4x=7y+20}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{6x-6y=6}\\{4x=7y-20}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{6x+6=6y}\\{4x-4y=3y-20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{6x-6=6y}\\{4x-4y=3y+20}\end{array}\right.$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $(\sqrt{-3}{)^2}=-3$ | B. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | C. | $\sqrt{4}=±2$ | D. | $\sqrt{27}÷\sqrt{3}=3$ |
| A. | xy | B. | 2a2b | C. | x2y | D. | -2x2yz |