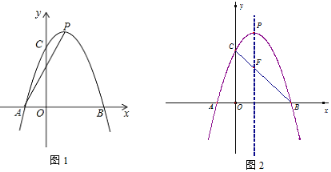��Ŀ����
����Ŀ����ͼ������ABC�У���O�DZ�AC��һ�����㣬��O��ֱ��MN��BC����MN����ACB��ƽ�����ڵ�E������ABC����ǡ�ACD��ƽ�����ڵ�F.
(1)̽���߶�EF��OC��������ϵ��˵�����ɣ�
(2)����O�˶����δ�������ABC����ʲô����ʱ���ı���AECF�������Σ���˵�����ɣ�
(3)����O�ڱ�AC���˶�ʱ���ı���BCFE________�����λ�������(����������������������)����˵�����ɣ�

���𰸡���1��![]() ����2������
����2������![]() �˶���
�˶���![]() ���е㣬��
���е㣬��![]() ����
����![]() Ϊֱ�ǵ�ֱ��������ʱ���ı���
Ϊֱ�ǵ�ֱ��������ʱ���ı���![]() �������Σ���3��������.
����������3��������.
��������
��1����ֱ��![]() ��
��![]() ��
��![]() ��ƽ�����ڵ�
��ƽ�����ڵ�![]() ����
����![]() �����ƽ�����ڵ�
�����ƽ�����ڵ�![]() ����֤��
����֤��![]() ��
��![]() �ǵ��������Σ����֤��
�ǵ��������Σ����֤��![]() ��
��
��2�������ε��ж����⣬�ı���![]() ���������Σ�����жԽ���
���������Σ�����жԽ���![]() ������
������![]() Ϊ
Ϊ![]() ���е㣬�ı���
���е㣬�ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() �У���
�У���![]() ʱ����öԽ����ഹֱ����������Ϊ�����Σ�
ʱ����öԽ����ഹֱ����������Ϊ�����Σ�
��3�����ε��ж����⣬��ʹ���Σ��������������ȣ��Խ����ഹֱ��
�⣺��1��![]() ���������£�
���������£�
![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�
![]() ��
��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
ͬ���ɵã�![]() ��
��
![]() ��
��
��![]() .
.
��2������![]() �˶���
�˶���![]() ���е㣬��
���е㣬��![]() ����
����![]() Ϊֱ�ǵ�ֱ��������ʱ���ı���
Ϊֱ�ǵ�ֱ��������ʱ���ı���![]() �������Σ��������£�
�������Σ��������£�
![]() ����
����![]() �˶���
�˶���![]() ���е�ʱ��
���е�ʱ��![]() ��
��
��![]() ��
��
![]() �ı���
�ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ��
��
![]() ��
��
![]() ����
����![]() ��
��
![]() �ı���
�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��֪![]() ����
����![]() ����
����
![]() ��
��
![]() ��
��
![]() �ı���
�ı���![]() �������Σ�
��������
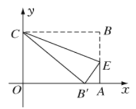
��3�������ܣ��������£���ͼ��

![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ��
��
![]() ��
��
���ı���![]() �����Σ���
��������![]() ��
��
����![]() �У������ܴ���������Ϊ
�У������ܴ���������Ϊ![]() �����Բ�������Ϊ���Σ�
�����Բ�������Ϊ���Σ�
�ʴ�Ϊ�������ܣ�

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�����Ŀ��ijУ��չ���ж�ʫ�ʾ��䣬���ﴫͳ�Ļ���ʫ���ж����Ϊ�˽���꼶ѧ������λ�е�ʫ���б�����������ȡ��30�����꼶ѧ�������顰һ��ʫ���б����������������ʾ��
һ��ʫ���б��������ף� | 2 | 3 | 4 | 5 | 6 | 7 |
�������ˣ� | 1 | 3 | 5 | 9 | 10 | 2 |
��1��������30��ƽ��ÿ��һ���б�ʫ�ʶ����ף�
��2����У���꼶����600��ѧ���μ�����λ������λ�У����ư��꼶ѧ����һ���б�ʫ��6�����ϣ���6�ף���ѧ���ж����ˣ�