题目内容
 如图,△DAE在平面直角坐标系中,∠DAE=90°,正方形网格上的单位长度是1.
如图,△DAE在平面直角坐标系中,∠DAE=90°,正方形网格上的单位长度是1.
(1)写出点A、D、E的坐标.
(2)画出△DAE绕点D逆时针旋转90°后得到的△DCF(∠C=90°).再画出△DCF沿DA方向平移6个单位长度后得到的△ABH(∠B=90°).
(3)线段AH与ED交于点G,求AG的长.
 解:(1)如图所示:A(2,8),D(8,8),E(2,5);
解:(1)如图所示:A(2,8),D(8,8),E(2,5);(2)如图所示,△DCF,△ABH为所求;
(3)∵△DAE绕点D逆时针旋转90°后得到的△DCF,
∴∠EDF=90°,
∵△DCF沿DA方向平移6个单位长度后得到的△ABH,
∴AH⊥FD,
∴∠EGH=∠EDF=90°,
∴AH⊥ED,
∵∠BAH=∠GAE,
∴△AEG∽△AHB,
∴
 =
= ,
,∵AE=3,AH=3
 ,AB=6,
,AB=6,∴
 =
= ,
,解得:AG=
 .
.分析:(1)根据坐标系得出各点坐标即可;
(2)根据旋转对称图形以及平移图形的作法找出对应点坐标连接作出即可;
(3)根据旋转对称图形的性质、勾股定理可知线段AH与DE的位置关系,利用相似三角形的判定与性质可求AG的长.
点评:本题考查了作旋转对称图形及旋转对称图形的性质同时考查了勾股定理及相似三角形的判定与性质等知识,根据已知得出△AEG∽△AHB是解题关键.

练习册系列答案
相关题目
 如图,△DAE在平面直角坐标系中,∠DAE=90°,正方形网格上的单位长度是1.
如图,△DAE在平面直角坐标系中,∠DAE=90°,正方形网格上的单位长度是1. (2012•上海)如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(-1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=
(2012•上海)如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(-1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=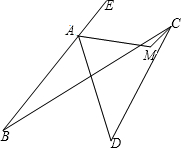 如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=
如图,平面内,四条线段AB、BC、CD、DA首尾顺次相接,∠B=24°,∠D=42°,点E在BA的延长线上,∠DAE的平分线和∠BCD的平分线相交于M,则∠AMC=