题目内容
如图，菱形ABCD，点E、F在对角线BD上，BE=DF=
BD，若四边形AECF为正方形，则tan∠ABE=_________．
BD，若四边形AECF为正方形，则tan∠ABE=_________．
连接AC交BD于点O．根据正方形的性质知：AC⊥BD．设正方形的边长为2a，可求出AO，EF的长，再根据BE="DF=" 
BD，可将AO的长求出，代入tan∠ABE= 
计算即可．
解：连接AC交BD于点O．
设正方形AECF的边长为2a，则EF=2
a，AO=
EF=a．
∵BE=DF=BD，
∴EF=BD．
∵BD=4a，BO=BD=2a，
∴tan∠ABE==
=．
本题综合考查菱形和正方形性质的应用和运算．
BD，可将AO的长求出，代入tan∠ABE= 计算即可．解：连接AC交BD于点O．
设正方形AECF的边长为2a，则EF=2
a，AO=EF=a．∵BE=DF=
BD，∴EF=
BD．∵BD=4
a，BO=BD=2a，∴tan∠ABE=
==．本题综合考查菱形和正方形性质的应用和运算．
练习册系列答案
名校课堂系列答案
相关题目
，
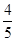
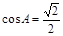，则这个三角形一定是……（ ）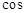
В是关于x的方程kx2－kx+1=0的两个根,求∠B的度数. (11分)
中，
是斜边
上的中线，已知，
，则
的值是（ ）
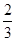
km的C处．
是∠B的