题目内容
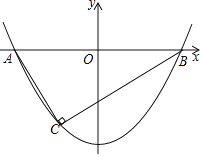
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的表达式;
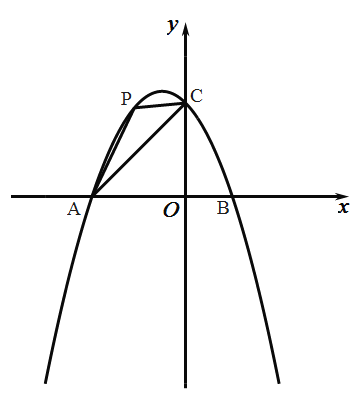
(2)点![]() 是抛物线上第二象限内的点,连接
是抛物线上第二象限内的点,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
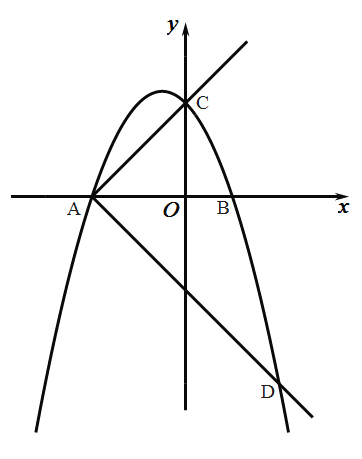
(3)作射线![]() ,将射线
,将射线![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 交抛物线于另一点
交抛物线于另一点![]() ,在射线
,在射线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小.若存在,求出
的周长最小.若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() (3)存在,点
(3)存在,点![]() 坐标为
坐标为![]()
【解析】
(1)用待定系数法即可求抛物线的表达式;
(2)过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,设
,设![]()
将点D的坐标用含x的代数式表示出来,然后利用![]()
![]() 即可求出面积最大时的x的值,从而确定点P的坐标;
即可求出面积最大时的x的值,从而确定点P的坐标;
(3)延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交点即为满足条件的点
交点即为满足条件的点![]() .分别求出AD,
.分别求出AD,![]() 的直线解析式,然后建立方程组即可求出交点H的坐标.
的直线解析式,然后建立方程组即可求出交点H的坐标.
解:(1)将![]() 、
、![]() 和
和![]() 代入
代入![]() 得,
得,
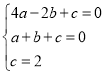 解得:
解得: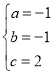
∴抛物线的表达式为![]() .
.
(2)如图,过点![]() 作
作![]() 轴,交线段
轴,交线段![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
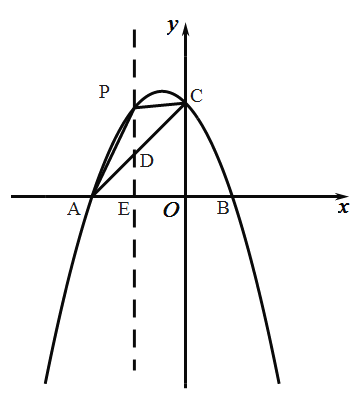
设![]()
∵![]()
∴![]() ,
,
∴直线![]() 解析式为
解析式为![]()
∴![]()
∴![]()
由图可得
![]()
![]()
![]()
![]()
∵![]()
∴![]()
![]()
![]()
![]()
当![]() 时
时![]() 最大
最大![]()
将![]() 代入
代入![]() 得
得
![]()
∴![]() .
.
(3)在射线![]() 上存在一点
上存在一点![]() ,使
,使![]() 的周长最小.
的周长最小.
如图,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() 与
与![]() 交点即为满足条件的点
交点即为满足条件的点![]() .
.
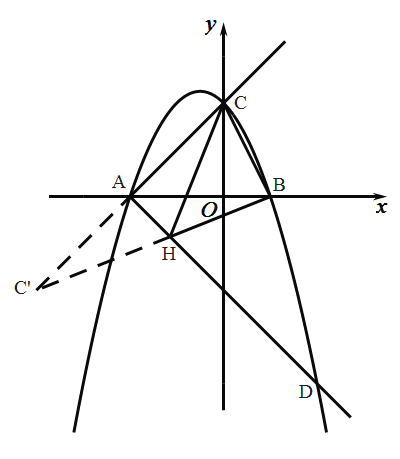
∵射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得射线
得射线![]()
∴![]()
∴![]()
∴直线![]() 解析式为
解析式为![]()
∵![]()
∴![]() ,
,![]() 垂直平分
垂直平分![]()
∴![]()
∴当![]() 在同一直线上时,
在同一直线上时,
![]() 最小.
最小.
设直线![]() 解析式为
解析式为![]() ,
,
将![]() 代入
代入
得![]() 解得
解得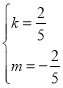
∴直线![]()
∵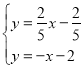 解得:
解得: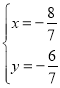
∴点![]() 坐标为
坐标为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目