题目内容
如图,花园边墙上有一宽为lm的矩形门ABCD,量得门框对角线AC的长为2m,现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是 m2.(精确到0.01m2,л≈3.14, ≈1.73)
≈1.73)
【答案】分析:要打掉墙体的面积是圆的面积减矩形面积减弓形BC的面积.
解答: 解:在Rt△ABC中,
解:在Rt△ABC中,
∵AC=2m,BC=1m.
∴∠BAC=30°,BC=1m,AB= m.
m.
∴∠BOC=60°,即△OBC是等边三角形.
∠BOC所对的弧与弦BC所围成的弓形的面积S1= -
- =
= -
- (m2).
(m2).
∴要打掉的墙体的面积=S圆O-S矩形ABCD-S1=π- -(
-( -
- )=
)= -
- ≈1.32m2.
≈1.32m2.
点评:本题的关键是理解阴影部分的面积是由哪几部分图形组成的,然后利用公式求值.
解答:
 解:在Rt△ABC中,
解:在Rt△ABC中,∵AC=2m,BC=1m.
∴∠BAC=30°,BC=1m,AB=
 m.
m.∴∠BOC=60°,即△OBC是等边三角形.
∠BOC所对的弧与弦BC所围成的弓形的面积S1=
 -
- =
= -
- (m2).
(m2).∴要打掉的墙体的面积=S圆O-S矩形ABCD-S1=π-
 -(
-( -
- )=
)= -
- ≈1.32m2.
≈1.32m2.点评:本题的关键是理解阴影部分的面积是由哪几部分图形组成的,然后利用公式求值.

练习册系列答案
相关题目
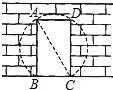 如图,花园边墙上有一宽为lm的矩形门ABCD,量得门框对角线AC的长为2m,现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是
如图,花园边墙上有一宽为lm的矩形门ABCD,量得门框对角线AC的长为2m,现准备打掉部分墙体,使其变为以AC为直径的圆弧形门,问要打掉墙体的面积是 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)
 ≈1.73)
≈1.73)