题目内容
若|p+2|与q2-8q+16互为相反数,分解因式(x2+y2)-(pxy+q)=________.
(x+y+2)(x+y-2)
分析:根据非负数的性质,由|p+2|+(q2-8q+16)=0,得|p+2|+(q-4)2=0,求出p,q的值是-2和4,代入代数式并整理,再利用分组分解法分解因式.
解答:依题意得|p+2|+(q2-8q+16)=0,即|p+2|+(q-4)2=0,
∴p+2=0,q-4=0,
解得p=-2,q=4,
∴(x2+y2)-(pxy+q),
=(x2+y2)-(-2xy+4),
=x2+y2+2xy-4,
=(x2+2xy+y2)-4,
=(x+y)2-22,
=(x+y+2)(x+y-2).
点评:本题考查了非负数的性质,分组分解法分解因式,先求出p、q的值,再代入数据整理是关键,利用三一分组进行因式分解.
分析:根据非负数的性质,由|p+2|+(q2-8q+16)=0,得|p+2|+(q-4)2=0,求出p,q的值是-2和4,代入代数式并整理,再利用分组分解法分解因式.
解答:依题意得|p+2|+(q2-8q+16)=0,即|p+2|+(q-4)2=0,
∴p+2=0,q-4=0,
解得p=-2,q=4,
∴(x2+y2)-(pxy+q),
=(x2+y2)-(-2xy+4),
=x2+y2+2xy-4,
=(x2+2xy+y2)-4,
=(x+y)2-22,
=(x+y+2)(x+y-2).
点评:本题考查了非负数的性质,分组分解法分解因式,先求出p、q的值,再代入数据整理是关键,利用三一分组进行因式分解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
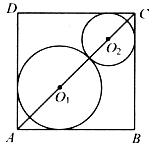
相关题目
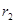 的关系式;
的关系式;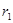 ,
,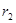 .
.
 ,
, .
.
 ,
, .
.