题目内容
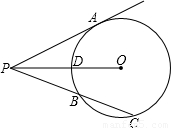
如图,设⊙O的半径为8,过圆外一点P引切线PA,切点为A,PA=6,C为圆周上一动点,PC交圆于另一点B,设PC=x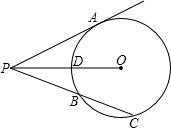 ,PB=y,且x>y.
,PB=y,且x>y.(1)试求:y关于x的函数解析式,并求出自变量x的取值范围;
(2)若cos∠OPC=
| 4 | 5 |
分析:(1)根据切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项,得出PA2=PB•PC,即可代入求出,再根据PA≤x≤PE,求出PE即可;
(2)首先利用已知条件,运用锐角三角函数求出PF,再利用勾股定理求出FO,FC,进而求出PC的长.
(2)首先利用已知条件,运用锐角三角函数求出PF,再利用勾股定理求出FO,FC,进而求出PC的长.
解答:解:(1)连接AO,
∵PA是⊙O的切线,切点为A,PBC是⊙O的割线,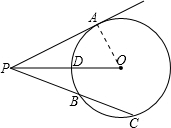
∴PA2=PB•PC,
∵PA=6,PC=x,PB=y,
∴36=xy,
整理得:y=
∵切线PA=6,PBC是⊙O的割线,
∴PA≤PC≤PE,
即PA≤x≤PE,
∴x≥6,
∵⊙O的半径为8,∴AO=8,
∵PA=6,
∴PO=
=10;
∴PE=10+8=18,
∴6≤x≤18;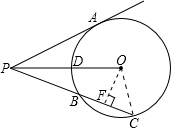
(2)过点O,作OF⊥PC于一点F,连接CO,
∵cos∠OPC=
,
∴cos∠OPC=
=
,
∵PO=10,
∴
=
,
∴PF=8,
在Rt△PFO中,
∴FO=
=
=6,
∵CO=8,FO=6,
∴CF=
=2
,
∴PC=x=PF+CF=8+2
.
∵PA是⊙O的切线,切点为A,PBC是⊙O的割线,

∴PA2=PB•PC,
∵PA=6,PC=x,PB=y,
∴36=xy,
整理得:y=
| 36 |
| x |
∵切线PA=6,PBC是⊙O的割线,
∴PA≤PC≤PE,
即PA≤x≤PE,
∴x≥6,
∵⊙O的半径为8,∴AO=8,
∵PA=6,
∴PO=
| 82+62 |
∴PE=10+8=18,
∴6≤x≤18;

(2)过点O,作OF⊥PC于一点F,连接CO,
∵cos∠OPC=
| 4 |
| 5 |
∴cos∠OPC=
| PF |
| PO |
| 4 |
| 5 |
∵PO=10,
∴
| PF |
| 10 |
| 4 |
| 5 |
∴PF=8,
在Rt△PFO中,
∴FO=
| PO2-PF2 |
| 102-82 |
∵CO=8,FO=6,
∴CF=
| 82-62 |
| 7 |
∴PC=x=PF+CF=8+2
| 7 |
点评:此题主要考查了切割线定理以及锐角三角函数和勾股定理的应用等知识,此题用到常用辅助线过圆心连接切点以及过圆心向弦作垂线等,基本思路都是构建直角三角形,利用勾股定理求出.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
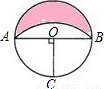
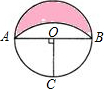 如图,设⊙O的半径为R,AB是⊙O的直径,OC为半径,OC⊥AB,以C为圆心,AC为半径作弧,则图中阴影部分的面积是
如图,设⊙O的半径为R,AB是⊙O的直径,OC为半径,OC⊥AB,以C为圆心,AC为半径作弧,则图中阴影部分的面积是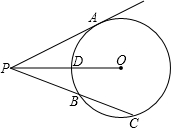 ,PB=y,且x>y.
,PB=y,且x>y.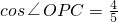 时,求x的值.
时,求x的值.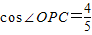 时,求x的值.
时,求x的值.