题目内容
已知抛物线![]() 经过点(1,2)。
经过点(1,2)。
(1)若a=1,抛物线顶点为A,它与x轴交于两点B、C,且⊿ABC为等边三角形,
求b的值;
(2)若abc=4,且a≥b≥c,求 |a| + |b| + |c| 的最小值。
解:⑴由题意,a+b+c=2, ∵a=1,∴b+c=1 抛物线顶点为A(-![]() ,c-
,c-![]() )
)
设B(x1,0),C(x2,0),∵x1+x2=-b,x1x2=c,△=b2-4c>0
∴|BC|=| x1-x2|=![]() =
=![]() =
=![]()
∵△ABC为等边三角形,∴![]() -c=
-c= ![]()
![]()
即b2-4c=2![]() ·
·![]() ,∵b2-4c>0,∴
,∵b2-4c>0,∴![]() =2
=2![]()
∵c=1-b, ∴b2+4b-16=0, b=-2±2![]() 所求b值为-2±2
所求b值为-2±2![]()
⑵∵a≥b≥c,若a<0,则b<0,c<0,a+b+c<0,与a+b+c=2矛盾.∴a>0.
∵b+c=2-a,bc=![]() ∴b、c是一元二次方程x2-(2-a)x+
∴b、c是一元二次方程x2-(2-a)x+![]() =0的两实根.
=0的两实根.
∴△=(2-a)2-4×![]() ≥0, ∴a3-4a2+4a-16≥0, 即(a2+4)(a-4)≥0,故a≥4.
≥0, ∴a3-4a2+4a-16≥0, 即(a2+4)(a-4)≥0,故a≥4.
∵abc>0,∴a、b、c为全大于0或一正二负.
①若a、b、c均大于0,∵a≥4,与a+b+c=2矛盾;
②若a、b、c为一正二负,则a>0,b<0,c<0,
则|a|+|b|+|c|=a-b-c=a-(2-a)=2a-2,∵ a≥4,故2a-2≥6
当a=4,b=c=-1时,满足题设条件且使不等式等号成立.
故|a|+|b|+|c|的最小值为6.

练习册系列答案
相关题目
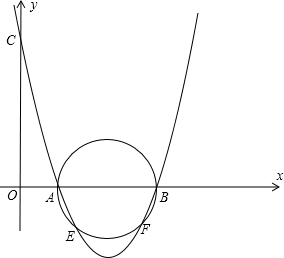 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆. 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.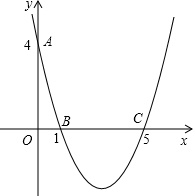 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.