Question

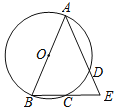
【题目】如图，点A，B，C，D在⊙O上，弦AD的延长线与弦BC的延长线相交于点E．用①AB是⊙O的直径，②CB＝CE，③AB＝AE中的两个作为题设，余下的一个作为结论组成一个命题，则组成真命题的个数为（　　）

A.0B.1C.2D.3

Answer 1

【答案】D

【解析】

根据题意和图形，可以写出其中的两个为题设，一个为结论时的命题是否为真命题，然后写出理由即可．

解：当①②为题设时，③为结论，这个命题是真命题，

理由：

连接AC

∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠ACB＝∠ACE＝90°，

在△ACB和△ACE中，

，

∴△ACB≌△ACE（SAS），

∴AB＝AE；

当①③为题设，②为结论时，这个命题是真命题，

理由：∵AB是⊙O的直径，

∴∠ACB＝90°，

∴∠ACB＝∠ACE＝90°，

在Rt△ACB和Rt△ACE中，

，

∴Rt△ACB≌Rt△ACE（HL），

∴CB＝CE；

当②③为题设，①为结论时，这个命题是真命题，

理由：在△ACB和△ACE中，

，

∴△ACB≌△ACE（SSS），

∴∠ACB＝∠ACE，

又∵∠ACB+∠ACE＝180°，

∴∠ACB＝∠ACE＝90°，

∴AB是⊙O的直径；

故选：D．