题目内容
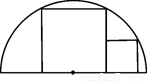
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A.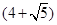 cm B.9 cm
C.
cm B.9 cm
C. cm D.
cm D. 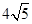 cm
cm
【答案】
D
【解析】
试题分析:

连接OA、OB、OE,
∵四边形ABCD是正方形,
∴AD=BC,∠ADO=∠BCO=90°,
∵在Rt△ADO和Rt△BCO中
∵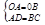 ,
,
∴Rt△ADO≌Rt△BCO,
∴OD=OC,
∵四边形ABCD是正方形,
∴AD=DC,
设AD=acm,则OD=OC= DC=
DC= AD=
AD= acm,
acm,
在△AOD中,由勾股定理得:OA=OB=OE=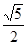 acm,
acm,
∵小正方形EFCG的面积为16cm2,
∴EF=FC=4cm,
在△OFE中,由勾股定理得: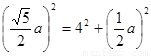 ,
,
解得:a=-4(舍去),a=8,
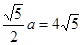 (cm),
(cm),
故选D.
考点:垂径定理;勾股定理.
点评:本题考查了全等三角形的性质和判定,勾股定理的应用,主要考查学生运用定理进行计算的能力,用的数学思想是方程思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
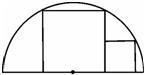 如图,两正方形彼此相邻且内接于半圆,若半圆的半径为5cm,则小正方形的边长为( )
如图,两正方形彼此相邻且内接于半圆,若半圆的半径为5cm,则小正方形的边长为( )| A、2cm | ||||
| B、2.5cm | ||||
C、
| ||||
D、
|
如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )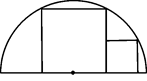
A.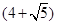 cm cm | B.9 cm | C.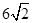 cm cm | D.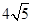 cm cm |
 (2011•津南区一模)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为
(2011•津南区一模)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为