题目内容
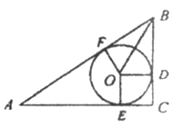
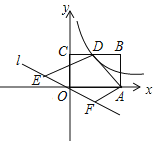
【题目】如图，函数y= 
(x>0)的图象与矩形OABC的边BC交于点D，分别过点A，D作AF∥DE，交直线y=k2x(k2<0)于点F，E.若OE=OF，BD=2CD，四边形ADEF的面积为12，则k1的值为________.
【答案】4
【解析】
如图，连接OD，过O作OM∥ED交AD于M，可以得出S△AOD=
S四边形ADEF，进而得到S矩形OACB的值．作DH⊥OA于H，可得S矩形OCDH，从而得到结论．
解：如图，连接OD，过O作OM∥ED交AD于M．
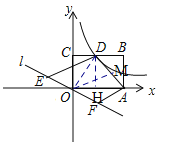
S△AOD=S△AOM+S△DOM=OM×h1+OM×h2==OM（h1+h2），S四边形ADEF=（AF+ED）h．
又∵OM=（AF+ED），h1+h2=h，故S△AOD=S四边形ADEF=×12=6．
∵△AOD和矩形OACB同底等高，故S矩形OACB=12，作DH⊥OA于H．
∵ BD=2CD ，BC=3CD，故S矩形OCDH=
×12=4，即CD×DH=xy=k1=4．
故答案为：4．
练习册系列答案
阅读快车系列答案
相关题目
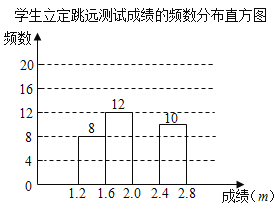
【题目】为了解某校八年级学生立定跳远水平，随机抽取该年级50名学生进行测试，并把测试成绩（单位：
）绘制成不完整的频数分布表和频数分布直方图.
学生立定路远测试成绩的频数分布表
分组 | 频数 |
|
|
| 12 |
|
|
| 10 |
请根据图表中所提供的信息，完成下列问题：
（1）求表中
，
的值；
（2）请把频数分布直方图补充完整；
（3）该校八年级共有800名学生，估计该年级学生立定跳远成绩在
范围内的学生有多少人？
