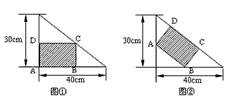
题目内容
 有一块直角三角形铁皮,两条直角边长分别为30cm和40cm,现需在其内部裁出一块面积尽量大的矩形铁皮ABCD,设矩形铁皮的一边AB=xcm.当x取何值时,矩形铁皮的面积最大?最大值是多少?
有一块直角三角形铁皮,两条直角边长分别为30cm和40cm,现需在其内部裁出一块面积尽量大的矩形铁皮ABCD,设矩形铁皮的一边AB=xcm.当x取何值时,矩形铁皮的面积最大?最大值是多少?分析:表示出矩形的长与宽,进而可表示出矩形面积,再利用配方法,求出最大值.
解答:解:如图,AF=40cm,AE=30cm,AB=xcm,则CD=xcm,
∵CD∥AF,
∴△EDC∽△EAF,
∴
=
,
∴
=
,
则DE=
x,
∴AD=30-
x,
则矩形铁皮的面积:
S=AD×AB=x×(30-
x)=-
x2+30x=-
(x-20)2+300(0<x<40),
则x=20时,最大面积为300cm2.
∵CD∥AF,
∴△EDC∽△EAF,
∴
| CD |
| AF |
| ED |
| AE |
∴
| x |
| 40 |
| DE |
| 30 |
则DE=
| 3 |
| 4 |
∴AD=30-
| 3 |
| 4 |
则矩形铁皮的面积:
S=AD×AB=x×(30-
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
则x=20时,最大面积为300cm2.
点评:本题考查了二次函数模型的构建以及相似三角形的性质与判定等知识,解题的关键是构建二次函数模型,利用配方法求函数的最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
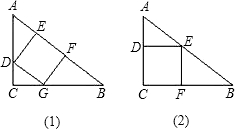 一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?
一个顶点在斜边上,如图(2).两种情形下正方形的面积哪个大?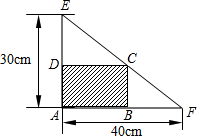 有一块直角三角形铁皮,两条直角边长分别为30cm和40cm,现需在其内部裁出一块面积尽量大的矩形铁皮ABCD,设矩形铁皮的一边AB=xcm.当x取何值时,矩形铁皮的面积最大?最大值是多少?
有一块直角三角形铁皮,两条直角边长分别为30cm和40cm,现需在其内部裁出一块面积尽量大的矩形铁皮ABCD,设矩形铁皮的一边AB=xcm.当x取何值时,矩形铁皮的面积最大?最大值是多少?